Question

If $3\cot A=4$, check whether $\dfrac{1-{{\tan }^{2}}A}{1+{{\tan }^{2}}A}={{\cos }^{2}}A-{{\sin }^{2}}A$ or not.

Answer 1

Hint : It is given that the value of $\cot A=\dfrac{4}{3}$ and we know that $\tan A$ is the reciprocal of $\cot A$ then we can write $\tan A=\dfrac{3}{4}$. Substitute this value of $\tan A$ in $\dfrac{1-{{\tan }^{2}}A}{1+{{\tan }^{2}}A}$ then evaluate it. From $\tan A$, find the values of $\sin A\And \cos A$ and then substitute the value of $\sin A$ and $\cos A$ in ${{\cos }^{2}}A-{{\sin }^{2}}A$. And then compare the L.H.S and R.H.S of the given equation.

Complete step by step solution :
We are asked to check whether,
$\dfrac{1-{{\tan }^{2}}A}{1+{{\tan }^{2}}A}={{\cos }^{2}}A-{{\sin }^{2}}A$ is true or not.
It is given that:
$\begin{aligned} & 3\cot A=4 \\\ & \Rightarrow \cot A=\dfrac{4}{3} \\\ \end{aligned}$
From the trigonometry, we know that $\tan A=\dfrac{1}{\cot A}$ so $\tan A=\dfrac{3}{4}$.
Now, we are going to substitute the above calculated value of $\tan A$ in $\dfrac{1-{{\tan }^{2}}A}{1+{{\tan }^{2}}A}$.
$\begin{aligned} & \dfrac{1-{{\left( \dfrac{3}{4} \right)}^{2}}}{1+{{\left( \dfrac{3}{4} \right)}^{2}}} \\\ & =\dfrac{1-\dfrac{9}{16}}{1+\dfrac{9}{16}} \\\ \end{aligned}$
$\begin{aligned} & \dfrac{16-9}{16+9} \\\ & =\dfrac{7}{25} \\\ \end{aligned}$
From the above calculated value of $\tan A$ we can determine the value of $\sin A\text{ and }\cos A$.
$\tan A=\dfrac{3}{4}$
To find the value of $\sin A\text{ and }\cos A$ we are drawing a right angled triangle in the below figure.

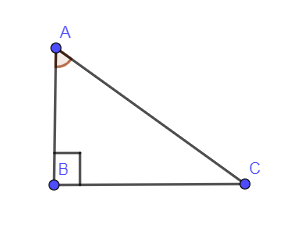
So from Pythagoras theorem we can find the values of $\sin A\text{ and }\cos A$.
And we know that $\tan A=\dfrac{P}{B}$, here “P” stands for perpendicular corresponding to angle A and “B” stands for the base corresponding to angle A.
$\tan A=\dfrac{3}{4}$
In the above equation, the value of P = 3 and the value of B = 4 so using Pythagoras theorem we can find the hypotenuse using the formula,
$\begin{aligned} & {{H}^{2}}={{P}^{2}}+{{B}^{2}} \\\ & \Rightarrow {{H}^{2}}={{3}^{2}}+{{4}^{2}} \\\ & \Rightarrow {{H}^{2}}=9+16=25 \\\ & \Rightarrow H=5 \\\ \end{aligned}$
From the trigonometric ratios we know that,
$\sin A=\dfrac{P}{H}$
Plugging the values of “P” and “H” in the above equation we get,
$\sin A=\dfrac{3}{5}$
$\cos A=\dfrac{B}{H}$
Plugging the values of “B” and “H” in the above equation we get,
$\cos A=\dfrac{4}{5}$
Substituting the values of $\sin A\text{ and }\cos A$ that we have just derived in ${{\cos }^{2}}A-{{\sin }^{2}}A$ we get,
$\begin{aligned} & \dfrac{16}{25}-\dfrac{9}{25} \\\ & =\dfrac{7}{25} \\\ \end{aligned}$
From the above calculation we got the value of ${{\cos }^{2}}A-{{\sin }^{2}}A$ is equal to $\dfrac{7}{25}$.
And we have also calculated above the value of $\dfrac{1-{{\tan }^{2}}A}{1+{{\tan }^{2}}A}$ is equal to $\dfrac{7}{25}$.
So, we can say that the equation given in question i.e. $\dfrac{1-{{\tan }^{2}}A}{1+{{\tan }^{2}}A}={{\cos }^{2}}A-{{\sin }^{2}}A$ is true because both L.H.S and R.H.S of this equation has the same value of $\dfrac{7}{25}$.

Note : The other way of stating the true and false of the statement given in the question is by having a sound understanding of the trigonometric identities.
$\dfrac{1-{{\tan }^{2}}A}{1+{{\tan }^{2}}A}={{\cos }^{2}}A-{{\sin }^{2}}A$
In the above equation, if you look carefully at the L.H.S of the equation you will find that it is equal to $\cos 2A$.
$\dfrac{1-{{\tan }^{2}}A}{1+{{\tan }^{2}}A}=\cos 2A$
And the R.H.S of the given equation is also $\cos 2A$ because:
${{\cos }^{2}}A-{{\sin }^{2}}A=\cos 2A$
As L.H.S = R.H.S so we can say that the statement $\dfrac{1-{{\tan }^{2}}A}{1+{{\tan }^{2}}A}={{\cos }^{2}}A-{{\sin }^{2}}A$ is true.
So, there is no need to use this equation $3\cot A=4$.