Question

If $3\cot A = 4$, check whether $\dfrac{{1 - {{\tan }^2}A}}{{1 + {{\tan }^2}A}} = {\cos ^2}A - {\sin ^2}A$ or not?

Answer 1

With the help of the condition given i.e. $3\cot A = 4$, figure out the trigonometric values which are needed and substitute In $\dfrac{{1 - {{\tan }^2}A}}{{1 + {{\tan }^2}A}} = {\cos ^2}A - {\sin ^2}A$, and check whether it satisfies or not.

Complete step-by-step answer:
Given that $3\cot A = 4$, Draw a right angled triangle and find the value needed, with the help of the values, figure out the trigonometric values needed.

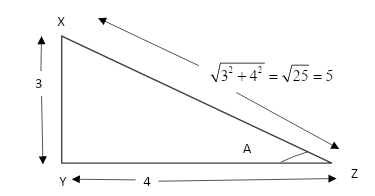
We know that $\cot A = \dfrac{{Adjacent\,side}}{{Opposite\,side}} = \dfrac{4}{3}$
Take $\dfrac{{1 - {{\tan }^2}A}}{{1 + {{\tan }^2}A}}$and substitute the value of $\tan A$, where $\tan A = \dfrac{3}{4}$
$\Rightarrow \dfrac{{1 - {{\tan }^2}A}}{{1 + {{\tan }^2}A}} \\\ \Rightarrow \dfrac{{1 - {{\left( {\dfrac{3}{4}} \right)}^2}}}{{1 + {{\left( {\dfrac{3}{4}} \right)}^2}}} \\\ \Rightarrow \dfrac{{1 - \left( {\dfrac{9}{{16}}} \right)}}{{1 + \left( {\dfrac{9}{{16}}} \right)}} \\\ \Rightarrow \dfrac{{\left( {\dfrac{{16 - 9}}{{16}}} \right)}}{{\left( {\dfrac{{16 + 9}}{{16}}} \right)}} \\\ \Rightarrow \dfrac{7}{{25}}.......\left( 1 \right) \\\$
Now take ${\cos ^2}A - {\sin ^2}A$and substitute the value of $\cos A$ and $\sin A$, where $\cos A = \dfrac{{Adjacent\,side}}{{{\text{Hypotenuse}}\,{\text{side}}}} = \dfrac{4}{5}$and $\sin A = \dfrac{{{\text{Opposite}}}}{{{\text{Hypotenuse}}}} = \dfrac{3}{5}$
$\Rightarrow {\cos ^2}A - {\sin ^2}A \\\ \Rightarrow {\left( {\dfrac{4}{5}} \right)^2} - {\left( {\dfrac{3}{5}} \right)^2} \\\ \Rightarrow \dfrac{{16}}{{25}} - \dfrac{9}{{25}} \\\ \Rightarrow \dfrac{7}{{25}}.......\left( 2 \right) \\\$
So, here from (1) and (2), both satisfy the equation. Hence, $\dfrac{{1 - {{\tan }^2}A}}{{1 + {{\tan }^2}A}} = {\cos ^2}A - {\sin ^2}A$.

Note: While solving trigonometric problems, know the values of trigonometric functions, it becomes easy while solving trigonometric problems. Try to draw the diagram while solving trigonometric problems.