Solveeit Logo
Login

Question

Question: If (3, – 4) and (– 6, 5) are the extremities of the diagonal of the parallelogram and (–2, 1) is its...

If (3, – 4) and (– 6, 5) are the extremities of the diagonal of the parallelogram and (–2, 1) is its third vertex, then its fourth vertex is,
(a) (– 1, 0)
(b) (0, – 1)
(c) (– 1, 1)
(d) None of these

Explanation

Solution

Here, in this question, first draw the parallelogram and mention the points. Use the principle of diagonals of parallelograms bisecting each other and hence the midpoint of both the diagonals is the same. Find the midpoint using the diagonal AC and then find the fourth vertex with the help of the given third vertex and the obtained midpoint.

Complete step-by-step answer:
Let us first draw the parallelogram with the given points and then find the fourth vertex of the parallelogram.

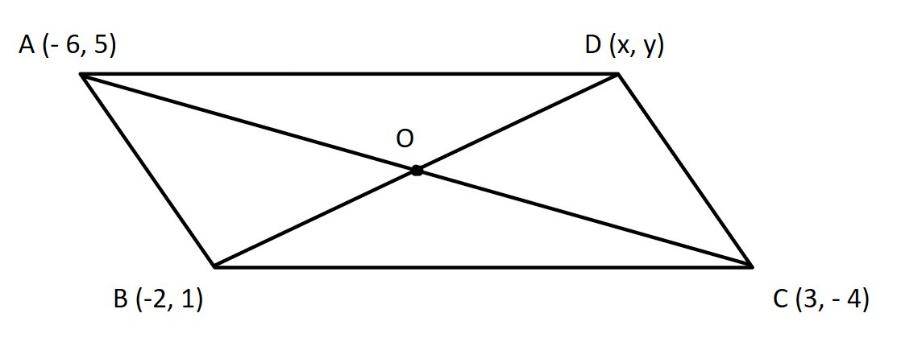
Here in the diagram we have taken the fourth vertex as D(x, y)\left( x,\,y \right).
Here, AC and BD are the diagonals of the parallelogram ABCD. Since, the diagonals of the parallelogram bisect each other, therefore, the midpoint O is the same for both the diagonals.
First let us find the midpoint O using the points A and C.
We know,
Midpoint O = (x1+x22, y1+y22)\left( \dfrac{{{x}_{1}}+{{x}_{2}}}{2},\,\dfrac{{{y}_{1}}+{{y}_{2}}}{2} \right)
We have, (x1,y1)=A(−6, 5)\left( {{x}_{1}},{{y}_{1}} \right)=\text{A}\left( -6,\,5 \right); (x2, y2)=C(3, −4)\left( {{x}_{2}},\,{{y}_{2}} \right)=\text{C}\left( 3,\,-4 \right)
Therefore, O = ((−6)+32, 5+(−4)2)\left( \dfrac{\left( -6 \right)+3}{2},\,\dfrac{5+\left( -4 \right)}{2} \right)
= (−6+32, 5−42)\left( \dfrac{-6+3}{2},\,\dfrac{5-4}{2} \right)
Midpoint, O = (−32, 12)\left( \dfrac{-3}{2},\,\dfrac{1}{2} \right)
Now, we know that the midpoint is the same for both the diagonals, therefore, O is also the midpoint of diagonal BD.
Here, we have, (x1,y1)=B(−2, 1)\left( {{x}_{1}},{{y}_{1}} \right)=\text{B}\left( -2,\,1 \right); (x2, y2)=D(x, y)\left( {{x}_{2}},\,{{y}_{2}} \right)=\text{D}\left( x,\,y \right)
Midpoint, O = (x1+x22, y1+y22)\left( \dfrac{{{x}_{1}}+{{x}_{2}}}{2},\,\dfrac{{{y}_{1}}+{{y}_{2}}}{2} \right)
(−32, 12)\left( \dfrac{-3}{2},\,\dfrac{1}{2} \right) = (−2+x2, 1+y2)\left( \dfrac{-2+x}{2},\,\dfrac{1+y}{2} \right)
Comparing the both the sides we will equate the xx coordinates and yy coordinates, we get
−32=−2+x2\dfrac{-3}{2}=\dfrac{-2+x}{2}
Multiply by 2 on both the sides of the equation, we get
−32×2=−2+x2×2\dfrac{-3}{2}\times 2=\dfrac{-2+x}{2}\times 2
−3=−2+x −3+2=x x=−1\begin{aligned} & -3=-2+x \\\ & -3+2=x \\\ & x=-1 \end{aligned}
Now, we have
12=1+y2\dfrac{1}{2}=\dfrac{1+y}{2}
Multiply by 2 on both the sides of the equation, we get
12×2=1+y2×2 1=1+y y=0\begin{aligned} & \dfrac{1}{2}\times 2=\dfrac{1+y}{2}\times 2 \\\ & 1=1+y \\\ & y=0 \end{aligned}
Hence, the fourth vertex is (x, y)\left( x,\,y \right)= (−1, 0)\left( -1,\,0 \right).

So, the correct answer is “Option A”.

Note: In this question, the parallelogram has two parallel sides with its opposite sides being equal. Unlike the diagonals of a rhombus which are perpendicular bisectors, the diagonals of a parallelogram are not perpendicular bisectors.