Question
Question: If $(2xy - y^2 - y)dx = (2xy + x - x^2)dy$ and $y(1) = 1$, then the value of $12|y(-1)|$ is...
If (2xy−y2−y)dx=(2xy+x−x2)dy and y(1)=1, then the value of 12∣y(−1)∣ is
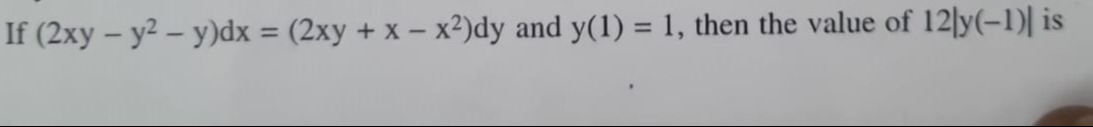
12
Solution
The given differential equation is (2xy−y2−y)dx=(2xy+x−x2)dy. We can rewrite this as (2xy−y2−y)dx−(2xy+x−x2)dy=0. Let M=2xy−y2−y and N=−(2xy+x−x2)=x2−2xy−x. We check if the differential equation is exact by verifying if ∂y∂M=∂x∂N. ∂y∂M=∂y∂(2xy−y2−y)=2x−2y−1. ∂x∂N=∂x∂(x2−2xy−x)=2x−2y−1. Since ∂y∂M=∂x∂N, the differential equation is exact.
For an exact differential equation Mdx+Ndy=0, there exists a function F(x,y) such that dF=Mdx+Ndy. This means ∂x∂F=M and ∂y∂F=N. We integrate M with respect to x to find F(x,y): F(x,y)=∫Mdx=∫(2xy−y2−y)dx=x2y−xy2−xy+g(y), where g(y) is an arbitrary function of y.
Now, we differentiate F(x,y) with respect to y and set it equal to N: ∂y∂F=∂y∂(x2y−xy2−xy+g(y))=x2−2xy−x+g′(y). We have N=x2−2xy−x. So, x2−2xy−x+g′(y)=x2−2xy−x. This implies g′(y)=0. Integrating with respect to y, we get g(y)=C1, where C1 is a constant.
The general solution is F(x,y)=C, which is x2y−xy2−xy+C1=C2. Let C=C2−C1. The general solution is x2y−xy2−xy=C.
We are given the initial condition y(1)=1. We substitute x=1 and y=1 into the general solution to find the value of C: (1)2(1)−(1)(1)2−(1)(1)=C 1−1−1=C C=−1.
The particular solution is x2y−xy2−xy=−1.
We need to find the value of 12∣y(−1)∣. Let y(−1)=y0. We substitute x=−1 into the particular solution: (−1)2y0−(−1)y02−(−1)y0=−1 1⋅y0−(−1)y02−(−1)y0=−1 y0+y02+y0=−1 y02+2y0+1=0 (y0+1)2=0 This gives y0=−1.
So, y(−1)=−1.
Finally, we need to find the value of 12∣y(−1)∣: 12∣y(−1)∣=12∣−1∣=12×1=12.
