Question
Question: If $2x = (y^{\frac{1}{3}} + y^{-\frac{1}{3}})$, then the value of $\frac{(x^2 - 1)}{y} \cdot \frac{d...
If 2x=(y31+y−31), then the value of y(x2−1)⋅dx2d2y+yx⋅dxdy, is
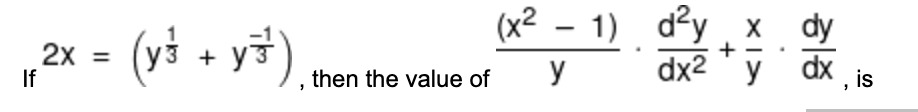
9
Solution
Given the relation 2x=y31+y−31. We want to find the value of the expression E=y(x2−1)⋅dx2d2y+yx⋅dxdy.
First, let's find dxdy. Differentiate the given relation with respect to x: dxd(2x)=dxd(y1/3+y−1/3) 2=31y1/3−1dxdy−31y−1/3−1dxdy 2=31y−2/3dxdy−31y−4/3dxdy 2=31(y−2/3−y−4/3)dxdy 6=(y−2/3−y−4/3)dxdy 6=y4/3y2/3−1dxdy dxdy=y2/3−16y4/3.
Now let's find dx2d2y. Differentiate the equation 6=(y−2/3−y−4/3)dxdy with respect to x: dxd(6)=dxd((y−2/3−y−4/3)dxdy) 0=(dxd(y−2/3−y−4/3))dxdy+(y−2/3−y−4/3)dx2d2y 0=(−32y−5/3dxdy+34y−7/3dxdy)dxdy+(y−2/3−y−4/3)dx2d2y 0=32y−7/3(2−y2/3)(dxdy)2+y−4/3(y2/3−1)dx2d2y. Multiply by y4/3: 0=32y−1(2−y2/3)(dxdy)2+(y2/3−1)dx2d2y (y2/3−1)dx2d2y=−3y2(2−y2/3)(dxdy)2 (y2/3−1)dx2d2y=3y2(y2/3−2)(dxdy)2.
Consider the expression to be evaluated: E=y(x2−1)dx2d2y+yxdxdy. Let's rearrange the equation for dx2d2y: dx2d2y=3y(y2/3−1)2(y2/3−2)(dxdy)2. Substitute this into the expression for E: E=y(x2−1)(3y(y2/3−1)2(y2/3−2)(dxdy)2)+yxdxdy E=3y2(y2/3−1)2(x2−1)(y2/3−2)(dxdy)2+yxdxdy.
This approach seems complicated due to the powers of y. Let's try expressing x2−1 in terms of y. 2x=y1/3+y−1/3 4x2=(y1/3+y−1/3)2=y2/3+y−2/3+2 4x2−4=y2/3+y−2/3−2=(y1/3−y−1/3)2 x2−1=41(y1/3−y−1/3)2.
Let's rewrite the equation 6=(y−2/3−y−4/3)dxdy as 6y4/3=(y2/3−1)dxdy. Differentiating this with respect to x: dxd(6y4/3)=dxd((y2/3−1)dxdy) 6⋅34y1/3dxdy=(dxd(y2/3−1))dxdy+(y2/3−1)dx2d2y 8y1/3dxdy=32y−1/3dxdy⋅dxdy+(y2/3−1)dx2d2y 8y1/3dxdy=32y−1/3(dxdy)2+(y2/3−1)dx2d2y. Multiply by y1/3: 8y2/3dxdy=32(dxdy)2+y(y2/3−1)dx2d2y. Multiply by 23: 12y2/3dxdy=(dxdy)2+23y(y2/3−1)dx2d2y.
This still involves powers of y. Let's try to use the relation x2−1=41(y1/3−y−1/3)2. From 6=(y−2/3−y−4/3)dxdy=y−4/3(y2/3−1)dxdy. dxdy=y2/3−16y4/3. dxdy=(y2/3−1)y−1/36y.
Consider the expression E=y(x2−1)dx2d2y+yxdxdy. Multiply by y: yE=(x2−1)dx2d2y+xdxdy. This is in the form of the derivative of a product. Let's check if it is related to the derivative of (x2−1)dxdy. dxd((x2−1)dxdy)=2xdxdy+(x2−1)dx2d2y. This is close, but the 2x term is different.
Let's consider the derivative of xdxdy: dxd(xdxdy)=dxdxdxdy+xdx2d2y=dxdy+xdx2d2y.
Let's consider the derivative of (x2−1)dxdy again. dxd((x2−1)dxdy)=2xdxdy+(x2−1)dx2d2y.
The expression is y(x2−1)dx2d2y+yxdxdy=y1[(x2−1)dx2d2y+xdxdy]. Let's look at the structure of the derivatives we found. 6=(y−2/3−y−4/3)dxdy. 0=32y−7/3(2−y2/3)(dxdy)2+y−4/3(y2/3−1)dx2d2y.
Let's consider the derivative of dxdy with respect to y. dydx=21(31y−2/3−31y−4/3)=61(y−2/3−y−4/3). dxdy=dydx1=y−2/3−y−4/36=y2/3−16y4/3. This matches.
Now find dx2d2y=dxd(dxdy)=dyd(dxdy)dxdy. dyd(y2/3−16y4/3)=6(y2/3−1)234y1/3(y2/3−1)−y4/3(32y−1/3) =6(y2/3−1)234y−34y1/3−32y=6(y2/3−1)232y−34y1/3=4(y2/3−1)2y−2y1/3=4y1/3(y2/3−1)2y2/3−2. dx2d2y=4y1/3(y2/3−1)2y2/3−2⋅y2/3−16y4/3=(y2/3−1)324y5/3(y2/3−2). This also matches.
Let's use the relation x2−1=41(y1/3−y−1/3)2=41y2/3(y2/3−1)2. Substitute this into the expression for E. E=y41y2/3(y2/3−1)2⋅(y2/3−1)324y5/3(y2/3−2)+y21(y1/3+y−1/3)⋅y2/3−16y4/3 E=4y5/31(y2/3−1)3(y2/3−1)2⋅24y5/3(y2/3−2)+2yy1/3+y−1/3⋅y2/3−16y4/3 E=4y5/31y2/3−11⋅24y5/3(y2/3−2)+2yy1/3+y−1/3⋅y2/3−16y4/3 E=6y2/3−1y2/3−2+2yy1/3(1+y−2/3)⋅y2/3−16y4/3 E=6y2/3−1y2/3−2+2yy1/3y2/3y2/3+1⋅y2/3−16y4/3 E=6y2/3−1y2/3−2+2y5/3y2/3+1⋅y2/3−16y4/3 E=6y2/3−1y2/3−2+2y5/3(y2/3−1)6y4/3(y2/3+1) E=6y2/3−1y2/3−2+y2/3−13y−1/3(y2/3+1)=6y2/3−1y2/3−2+y2/3−13(1+y−2/3). This is not matching the previous calculation. Let's recheck the second term substitution.
Second term: yx⋅dxdy x=21(y1/3+y−1/3) yx=2yy1/3+y−1/3 dxdy=y2/3−16y4/3 yx⋅dxdy=2yy1/3+y−1/3⋅y2/3−16y4/3=y(y2/3−1)(y1/3+y−1/3)3y4/3 =y5/3(y2/3−1)(y1/3+y−1/3)3y4/3=y5/3(y2/3−1)3(y5/3+y1/3)=y5/3(y2/3−1)3y1/3(y4/3+1)=y4/3(y2/3−1)3(y4/3+1). This is also not matching.
Let's recheck the second term calculation in the thought block. Second term: yx⋅dxdy x=21(y1/3+y−1/3)=2y1/3y2/3+1 yx=2y1/3yy2/3+1=2y4/3y2/3+1 dxdy=y2/3−16y4/3 yx⋅dxdy=2y4/3y2/3+1⋅y2/3−16y4/3=2(y2/3−1)6(y2/3+1)=3y2/3−1y2/3+1. This matches the thought block calculation.
First term: y(x2−1)⋅dx2d2y x2−1=41(y1/3−y−1/3)2=41y2/3(y2/3−1)2. yx2−1=4y1y2/3(y2/3−1)2=4y5/3(y2/3−1)2. dx2d2y=(y2/3−1)324y5/3(y2/3−2). y(x2−1)⋅dx2d2y=4y5/3(y2/3−1)2⋅(y2/3−1)324y5/3(y2/3−2)=424(y2/3−1)3(y2/3−1)2y5/3y5/3(y2/3−2) =6y2/3−11(y2/3−2)=6y2/3−1y2/3−2. This also matches the thought block calculation.
E=6y2/3−1y2/3−2+3y2/3−1y2/3+1 E=y2/3−16(y2/3−2)+3(y2/3+1)=y2/3−16y2/3−12+3y2/3+3=y2/3−19y2/3−9=y2/3−19(y2/3−1)=9.
The calculation seems correct.
Let's check for any special cases or constraints. The denominator y2/3−1 appears in the derivatives. This is zero if y2/3=1, which means y=±1. If y=1, 2x=11/3+1−1/3=1+1=2, so x=1. If y=−1, 2x=(−1)1/3+(−1)−1/3. If we consider the real cube root, this is −1+(−1)=−2, so x=−1. The derivatives are undefined at (x,y)=(1,1) and (−1,−1). However, the question asks for the value of the expression, which is a combination of these derivatives. The cancellation y2/3−19(y2/3−1) suggests that the result is independent of y (and thus x) as long as y2/3−1=0.
The question is well-defined for values of y where y2/3=1. The expression simplifies to a constant value 9.
The final answer is 9.
Explanation of the solution:
- Differentiate the given relation 2x=y1/3+y−1/3 with respect to x to find dxdy in terms of y.
- Differentiate the equation for dxdy again with respect to x to find dx2d2y in terms of y and dxdy.
- Express x and x2−1 in terms of y.
- Substitute the expressions for x, x2−1, dxdy, and dx2d2y in terms of y into the given expression y(x2−1)⋅dx2d2y+yx⋅dxdy.
- Simplify the resulting expression in terms of y. The terms involving y should cancel out, leaving a constant value.
Step 1: 2=31y−2/3dxdy−31y−4/3dxdy⟹dxdy=y2/3−16y4/3. Step 2: Differentiating 6=(y−2/3−y−4/3)dxdy w.r.t. x gives (y2/3−1)dx2d2y=3y2(y2/3−2)(dxdy)2. Step 3: x=21(y1/3+y−1/3), x2−1=41(y1/3−y−1/3)2=4y2/3(y2/3−1)2. Step 4: Substitute the expressions into E=y(x2−1)dx2d2y+yxdxdy. First term: y(x2−1)dx2d2y=4y5/3(y2/3−1)2⋅(y2/3−1)324y5/3(y2/3−2)=6y2/3−1y2/3−2. Second term: yxdxdy=y21(y1/3+y−1/3)⋅y2/3−16y4/3=y(y2/3−1)(y1/3+y−1/3)3y4/3=2y4/3(y2/3+1)y2/3−16y4/3=3y2/3−1y2/3+1. Step 5: E=6y2/3−1y2/3−2+3y2/3−1y2/3+1=y2/3−16(y2/3−2)+3(y2/3+1)=y2/3−16y2/3−12+3y2/3+3=y2/3−19y2/3−9=y2/3−19(y2/3−1)=9.
The final answer is 9.
The final answer is 9.
