Solveeit Logo
Login

Question

Question: If 2(q-a) is the harmonic mean between (q-p) and (q-r) then the quantities (p-a), (q-a) and (r-a) ar...

If 2(q-a) is the harmonic mean between (q-p) and (q-r) then the quantities (p-a), (q-a) and (r-a) are in:

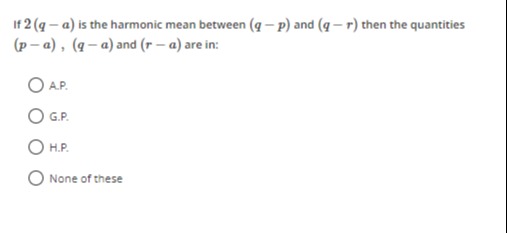
A

A.P.

B

G.P.

C

H.P.

D

None of these

Answer

G.P.

Explanation

Solution

The harmonic mean (HM) of two numbers A and B is given by H=2ABA+BH = \frac{2AB}{A+B}. Given that 2(q−a)2(q-a) is the harmonic mean between (q−p)(q-p) and (q−r)(q-r), we have: 2(q−a)=2(q−p)(q−r)(q−p)+(q−r)2(q-a) = \frac{2(q-p)(q-r)}{(q-p) + (q-r)} Dividing by 2: (q−a)=(q−p)(q−r)(q−p)+(q−r)(q-a) = \frac{(q-p)(q-r)}{(q-p) + (q-r)} Let X=p−aX = p-a, Y=q−aY = q-a, and Z=r−aZ = r-a. Then: q−p=(q−a)−(p−a)=Y−Xq-p = (q-a) - (p-a) = Y - X q−r=(q−a)−(r−a)=Y−Zq-r = (q-a) - (r-a) = Y - Z Substituting these into the equation: Y=(Y−X)(Y−Z)(Y−X)+(Y−Z)Y = \frac{(Y-X)(Y-Z)}{(Y-X) + (Y-Z)} Y[(Y−X)+(Y−Z)]=(Y−X)(Y−Z)Y[(Y-X) + (Y-Z)] = (Y-X)(Y-Z) Y(2Y−X−Z)=Y2−YZ−YX+XZY(2Y - X - Z) = Y^2 - YZ - YX + XZ 2Y2−XY−YZ=Y2−YZ−YX+XZ2Y^2 - XY - YZ = Y^2 - YZ - YX + XZ Y2=XZY^2 = XZ This condition implies that X,Y,ZX, Y, Z are in Geometric Progression (G.P.).