Question
Question: If $2^{|\ln x-2|}=\frac{4}{2^{|\ln x|}}$, then complete set of values of x is...
If 2∣lnx−2∣=2∣lnx∣4, then complete set of values of x is
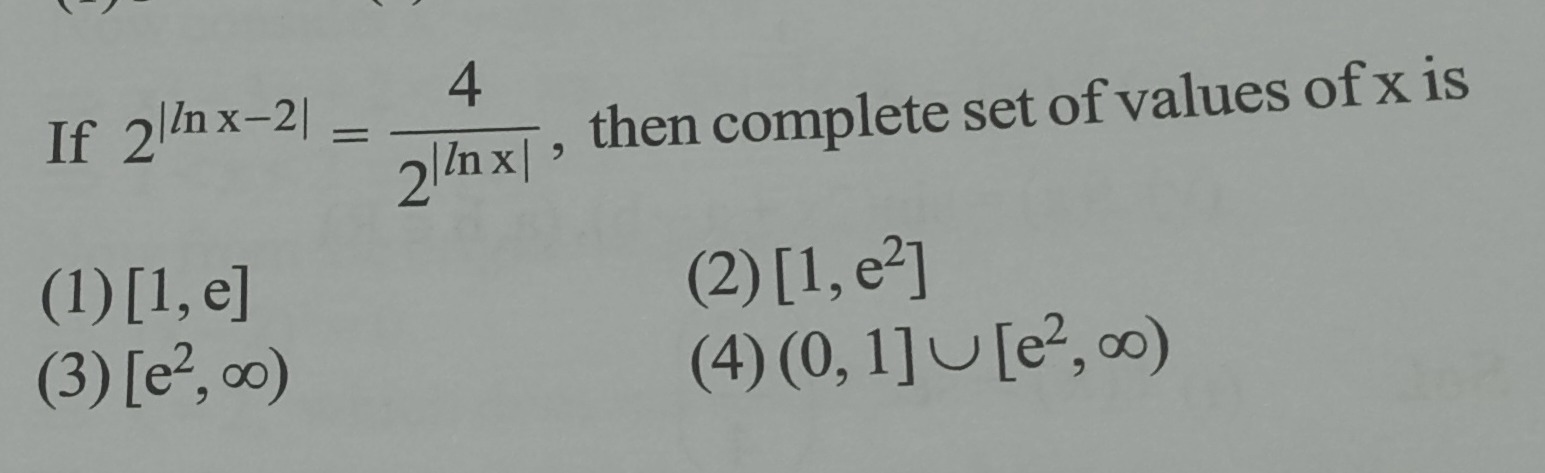
[1, e]
[1,e2]
[e2,∞)
(0,1]∪[e2,∞)
[1,e2]
Solution
The given equation is 2∣lnx−2∣=2∣lnx∣4.
The domain of the equation requires x>0 for lnx to be defined.
We can rewrite the equation as: 2∣lnx−2∣⋅2∣lnx∣=4
Using the property am⋅an=am+n, we have: 2∣lnx−2∣+∣lnx∣=4
Since 4=22, we can equate the exponents: ∣lnx−2∣+∣lnx∣=2
Let y=lnx. The equation becomes: ∣y−2∣+∣y∣=2
This equation involves the sum of two absolute values. We can solve this by considering cases based on the values of y where the expressions inside the absolute values change sign, i.e., y=0 and y=2.
Case 1: y<0 In this case, y−2<0 and y<0. So, ∣y−2∣=−(y−2)=2−y and ∣y∣=−y. The equation becomes (2−y)+(−y)=2, which simplifies to 2−2y=2. Subtracting 2 from both sides gives −2y=0, so y=0. This solution y=0 contradicts the condition y<0. Thus, there are no solutions in this case.
Case 2: 0≤y<2 In this case, y−2<0 and y≥0. So, ∣y−2∣=−(y−2)=2−y and ∣y∣=y. The equation becomes (2−y)+y=2, which simplifies to 2=2. This is an identity, which means that the equation is true for all values of y in the interval [0,2).
Case 3: y≥2 In this case, y−2≥0 and y≥0. So, ∣y−2∣=y−2 and ∣y∣=y. The equation becomes (y−2)+y=2, which simplifies to 2y−2=2. Adding 2 to both sides gives 2y=4, so y=2. This solution y=2 satisfies the condition y≥2. Thus, y=2 is a solution.
Combining the solutions from all cases, the values of y that satisfy ∣y−2∣+∣y∣=2 are all y such that 0≤y<2 or y=2. This is the interval [0,2]. So, 0≤y≤2.
Alternatively, we can interpret ∣y−2∣+∣y∣ geometrically as the sum of the distances from y to 2 and from y to 0 on the number line. The equation ∣y−2∣+∣y∣=2 means that the sum of the distances from y to 0 and 2 is equal to the distance between 0 and 2 (which is ∣2−0∣=2). This is true if and only if y lies on the line segment between 0 and 2, inclusive. Thus, 0≤y≤2.
Now we substitute back y=lnx: 0≤lnx≤2
To solve for x, we exponentiate the inequality using base e. Since e>1, the exponential function eu is increasing, so the inequality signs are preserved: e0≤elnx≤e2 1≤x≤e2
We must also consider the domain of the original equation, which is x>0. The interval [1,e2] is a subset of (0,∞), so all values in this interval are valid solutions.
The complete set of values of x is [1,e2].
