Question

If 28cosA + 45sinA=53, then 53sinA=55. State whether the given statement is true or false.

Answer 1

Hint: Focus on the point that the value of sinA can have a maximum value of 1 and for the equation 53sinA=55 to be true, sinA must be greater than 1.

Complete step-by-step answer:
Before moving to the solution, let us discuss the sine and cosine function, which we would be using in the solution. All the trigonometric ratios, including sine and cosine, are periodic functions. We can better understand this using the graph of sine and cosine.
First, let us start with the graph of sinx.

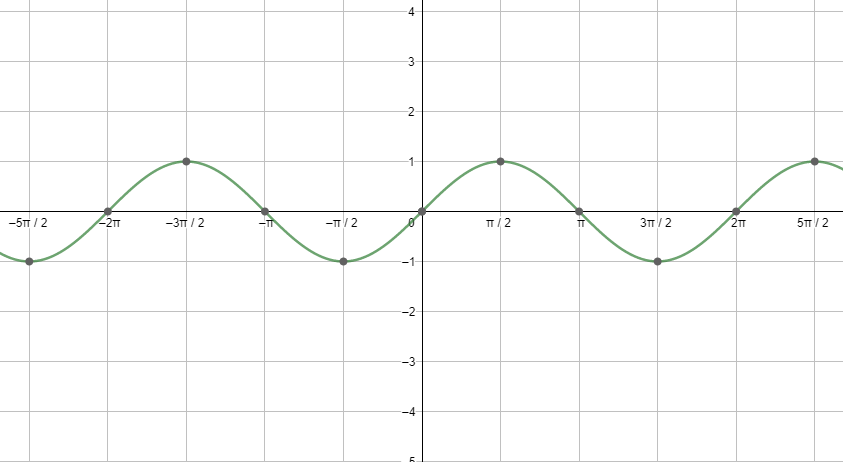
Next, let us see the graph of cosx.

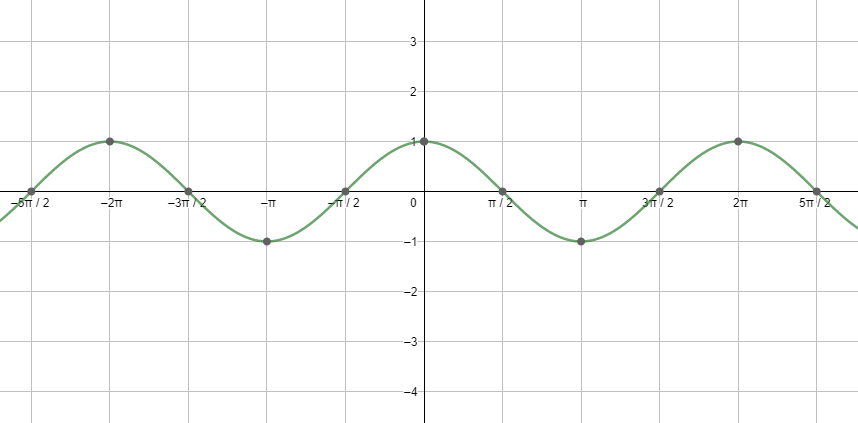
Similarly, we can draw the graphs of the other trigonometric ratios as well, and the graphs of the trigonometric ratios are very useful as well. Also, looking at the above graphs we can say that the maximum value of the function sinx and cosx is 1.
Now moving to the solution to the above question. We know that the maximum value of the function sinx and cosx is 1. So, the maximum value of 53sinA=53. But according to the question 53sinA=55, which is not possible.
So, we can conclude that the statement given in the question is false.

Note: It is possible that as soon as you see the question, without analysing you might start to simplify the 28cosA + 45sinA=53 and might end up getting nothing useful out of it. So, it is always a good habit to check the equations given in the question for domain and range of the known terms.