Question
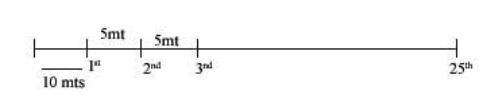
Question: If 25 trees are planted in a straight line at intervals of \[5\text{ }mts\] to water their gardener ...
If 25 trees are planted in a straight line at intervals of 5 mts to water their gardener must bring water for each tree separately from a well 10 mts from the first tree in line with the trees. Let d be the distance we have to cover in order to water all the trees beginning with the first if he starts from the well, find the sum of digits of d?
Solution
There are 24 gaps of 5 mts between 25 trees and well is 10 meter away from the 1st tree. So, we can say from 1st tree we can distance is 10 mts from 2nd tree he has travel 10mts back & them 15 mts to reach the 2nd tree total to(10+15) = 25 . Similarly for 3rd he has to travel 15mts & there 20 mts to water the 3rd tree the total (15+20)=35mts for 4th 20mts back & 25mts from well to tree = 20+25 = 45 mts & so on
Formula used:
Sn=2n=[2a+(n−1)d]
a = First term
d = common difference
n = Number of terms
Complete step-by-step answer:
__
Distance travel by gardener to water first tree = 10 m
Distance travel by gardener to water 2nd tree =T1W+WT2=10+15=25
Distance travel by gardener to water 3rd tree =T2W+WT3=15+20=35
Distance travel by gardener to water 4th tree=T3W+WT4=20+25=45
d= 10 + 25 + 35 + 45 + ……. upto 25th tree
Snd = 10 + [25 + 35 + 45 + ……. upto 25 trees]
= 10=225=[2x25+(24−1)x10]
Here we Q are using formula
Sn=2n=[2a+(n−1)d]
A = 25 i.e the first term
D = common difference i.e difference between two terms i.e. = 10
=10+[50+23x10]
=10+12x [50+230]
=10+12 x 280
=10+3360
= 3370
So, the sum of digits is d=3+3 +7+0=13
Note: Here we have to rate that there are 25 gaps between well and 25 trees whereas the gap between first tree & well is 10th and gaps between 25 trees are equal in distance of 5 mts are in total of 24 gaps. These are always out less gap than the number of things.
