Question
Question: If (2,−8) is one end of focal chord of the parabola \({{\text{y}}^2} = 32{\text{x}}\), then the othe...
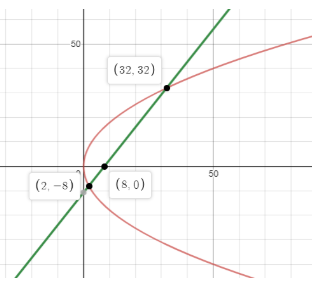
If (2,−8) is one end of focal chord of the parabola y2=32x, then the other end of the focal chord, is
A. (32,32)
B. (32, −32)
C. (−2,8)
D. (2,8)
Solution
Hint- Proceed the solution of this question first by comparing it with general parabola hence find the focal point then consider a general point on the parabola in terms of t then find the value of t with known coordinates hence t is known we can find other end coordinates too. Use the relation between parametric coordinates of the focal chord that is ⇒t1t2=−1.
Complete step-by-step answer:
In this particular question it is given one end of focal chord of the parabola y2=32x
So on comparing it with general parabola equation y2=4.a.x
⇒32x = 4.a.x
On solving
⇒a = 8
As we can assume a general point (at2,2at) on the parabola y2=4.a.x
Vertex of parabola ≡ (0,0)
Hence we have to take two points on the parabola as extremities of the chord that we can assume as \left( {{\text{at}}_1^2,2{\text{a}}{{\text{t}}_1}} \right){\text{ & }}\left( {{\text{at}}_2^2,2{\text{a}}{{\text{t}}_2}} \right)
If the chord of the parabola which passes through the focus, then it is called the focal chord.
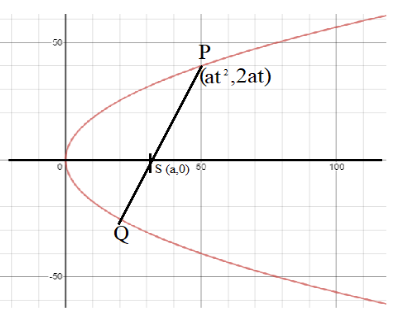
If y2=4ax be the equation of a parabola and (at12,2at1) a point P on it. Suppose the coordinates of the other extremity Q of the focal chord through P are (at22,2at2)
Then, PS and SQ, where S is the focus (a, 0), have the same slopes
so on equalising the slope of both line PS and SQ, we will get a condition of focal chord i.e.
⇒t1t2=−1 ………… (1)
Now we have a relation between {{\text{t}}_1}{\text{ & }}{{\text{t}}_2} so we can write coordinates of t2 in terms of t1 which will be
\Rightarrow {\text{at}}_2^2 = {\text{ a}}{\left( {\dfrac{1}{{{{\text{t}}_1}}}} \right)^2}{\text{ & }}2{\text{a}}{{\text{t}}_2} = 2{\text{a}}\left( {\dfrac{{ - 1}}{{{{\text{t}}_1}}}} \right) ……. (2)
So the coordinates of one end of focal chord of the parabola y2=32x given in the question which is (2,-8) so on comparing these with general coordinate (at12,2at1)
⇒at12=2,& 2at1=−8
on putting a= 8
⇒2.8t1=−8
⇒t1=2−1
Hence on putting value of t1 and a in equation (2) we can find the coordinates of other end of the focal chord
Therefore,
⇒at22= a(t11)2 = 8×(−2)2 = 32
2at2=2a2−1−1=2×8×2=32
Therefore, coordinates of other end of the focal chord will be (32, 32)
Hence, option A is correct.
Note- There is also an another approach to solve such type of particular question-
There is result , that we should have remember that, if \left( {{{\text{x}}_1},{{\text{y}}_1}} \right){\text{ & }}\left( {{{\text{x}}_2},{{\text{y}}_2}} \right) are two ends of focal chord of parabola y2=32x, then
⇒x1.x2=a2
Given equation of parabola-
⇒y2=32x
Vertex of parabola ≡ (0,0)
∴a=8
One end of the chord = (2, −8)
Let the other end of the chord be (x, y).
∴2.x=82
⇒x=32
Substituting the value of x in the given equation of the parabola, we have
y2=32.32
y = 32
As the one end of the focal chord is on (2, −8) hence the other end of the chord will be (32, 32).
Hence the focal cord and its extremities shown in below figure.