Question

If $15\cot {\text{A = 8}}$ is given to us , find $\sin {\text{A}}$ and $\sec {\text{A}}$.

Answer 1

In this question first we will manipulate the equation given in the equation. We will take $15$ on the R.H.S in denominator and then we will find the length of adjacent side and opposite side with the help of formula of $\cot$. Now, with the help of adjacent side and opposite side we will find the length of hypotenuse using Pythagoras theorem.

Complete step-by-step solution:
The information given in the question is $\cot {\text{A = }}\dfrac{{\text{8}}}{{15}}$. Therefore, from the given information we can say that Adjacent side $= 8$ and opposite side $= 15$ because we know that $\cot {\text{A = }}\dfrac{{{\text{Adjacent side}}}}{{{\text{opposite side}}}}$.

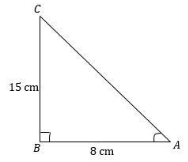
Now, we have to find out the hypotenuse of the right angle triangle with the help of the formula ${H^2} = {B^2} + {A^2}$where $H$ is hypotenuse, $B$ is the base and $A$ is the altitude of the triangle.
Now, {H^2} = {B^2} + {A^2}\\_\\_(1)
The value of $B = 8\,cm$ and the value of $A = 15\,cm$. Put this value in equation $(1)$
$\Rightarrow {H^2} = {8^2} + {15^2}$
We know that ${8^2} = 64$ and ${15^2} = 225$
$\Rightarrow {H^2} = 64 + 225 = 289$
We know that $289$ is the square of $17$. Therefore, we can write
$\Rightarrow H = \sqrt {289} = 17$
Therefore, we got the length of the hypotenuse of the right angle triangle is $17cm$.
From the figure we can say that the length of ${\text{AC}}$is $17cm$.
Now, with the help of the hypotenuse we will able to find the $\sin {\text{A}}$and $\sec {\text{A}}$
We know that $\sin {\text{A = }}\dfrac{{{\text{opposite side}}}}{{{\text{hypotenuse}}}}$. Therefore, we can write $\sin {\text{A = }}\dfrac{{{\text{BC}}}}{{{\text{AC}}}}$.
Therefore, we can write $\sin {\text{A = }}\dfrac{{{\text{BC}}}}{{{\text{AC}}}} = \dfrac{{15}}{{17}}$.
Similarly, We know that $\sec {\text{A = }}\dfrac{{{\text{hypotenuse}}}}{{{\text{Adjacent side}}}}$. Therefore, we can write $\sec {\text{A = }}\dfrac{{{\text{AC}}}}{{{\text{AB}}}}$.
Therefore, we can write $\sec {\text{A = }}\dfrac{{{\text{AC}}}}{{{\text{AB}}}} = \dfrac{{17}}{8}$.

Therefore, the answer is $\sin {\text{A = }}\dfrac{{15}}{{17}}$and $\sec {\text{A = }}\dfrac{{17}}{8}$.

Note: The important thing which we need is the formula of $\cot$ by which we can mark the sides of the right triangle and another important thing is the Pythagoras theorem. And be careful about the squares and square roots of the number while solving the Pythagoras theorem.
$\sin {\text{A = }}\dfrac{{{\text{Opposite}}}}{{{\text{Hypotenuse}}}}$
$\cos {\text{A = }}\dfrac{{{\text{Adjacent}}}}{{{\text{Hypotenuse}}}}$
$\tan {\text{A = }}\dfrac{{{\text{Opposite}}}}{{{\text{Adjacent}}}}$
$\cos ec {\text{A = }}\dfrac{{{\text{Hypotenuse}}}}{{{\text{Opposite}}}}$
$\sec {\text{A = }}\dfrac{{{\text{Hypotenuse}}}}{{{\text{Adjacent}}}}$
$\cot {\text{A = }}\dfrac{{{\text{Adjacent}}}}{{{\text{Opposite}}}}$