Question

If $10^{\log a (\log b (\log c x))} = 1$ and $10^{(\log b (\log c (\log a x)))} = 1$ then, a is equal to

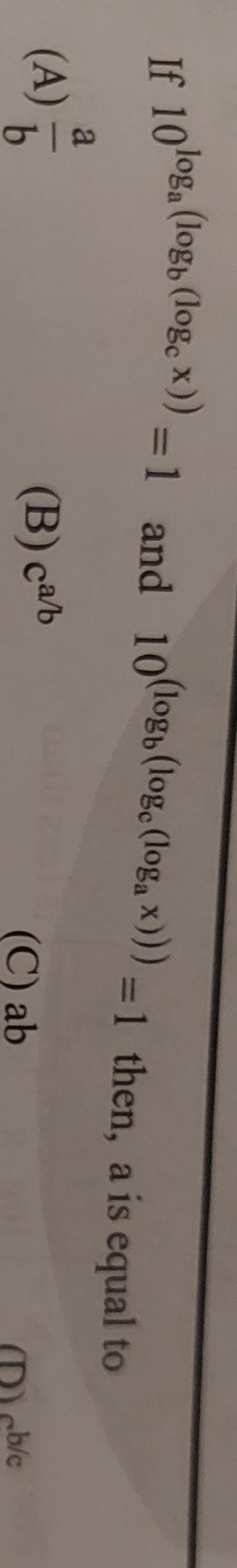
• A. $\frac{a}{b}$
• B. $c^{\frac{a}{b}}$
• C. ab
• D. $c^{\frac{b}{c}}$

Answer 1

Answer: (D)

$c^{\frac{b}{c}}$

Answer 2

Here's how to solve the problem:

1. Given Equations:

   $$10^{\log_a(\log_b(\log_c x))} = 1 \quad \text{and} \quad 10^{\log_b(\log_c(\log_a x))} = 1.$$

2. Step 1: Use the property $10^y=1 \implies y=0$.

   • From the first equation:

     $$\log_a(\log_b(\log_c x)) = 0 \implies \log_b(\log_c x) = 1 \quad (\text{since } \log_a 1=0).$$

   • From the second equation:

     $$\log_b(\log_c(\log_a x)) = 0 \implies \log_c(\log_a x) = 1.$$

3. Step 2: Convert logarithmic equations to exponential form.

   • For $\log_b(\log_c x) = 1$:

     $$\log_c x = b \quad \implies \quad x = c^b.$$

   • For $\log_c(\log_a x) = 1$:

     $$\log_a x = c \quad \implies \quad x = a^c.$$

4. Step 3: Equate the two expressions for $x$:

   $$a^c = c^b.$$

5. Step 4: Solve for $a$:

   Taking the $c^{\text{th}}$ root,

   $$a = \left(c^b\right)^{\frac{1}{c}} = c^{\frac{b}{c}}.$$

   Thus, the correct answer is $c^{\frac{b}{c}}$.