Question

If $0 < x < 1$ ,then \sqrt {1 + {x^2}} {\left[ {{{\left\\{ {x\cos \left( {{{\cot }^{ - 1}}x} \right) + \sin \left( {{{\cot }^{ - 1}}x} \right)} \right\\}}^2} - 1} \right]^{\dfrac{1}{2}}} =
A) $\dfrac{x}{{\sqrt {1 + {x^2}} }}$
B) $x$
C) $x\sqrt {1 + {x^2}}$
D) $\sqrt {1 + {x^2}}$

Answer 1

In this question, we have to find the value given expression. We proceed by considering, the inverse term $y = {\cot ^{ - 1}}x$ and solve it to find the value of $y = {\sin ^{ - 1}}\dfrac{1}{{\sqrt {1 + {x^2}} }}$ and $y = {\cos ^{ - 1}}\dfrac{x}{{\sqrt {1 + {x^2}} }}$. Now we put this value in the expression and simplify to find the required answer. We will also use the fact that $\cos \left( {{{\cos }^{ - 1}}\theta } \right) = \theta$ and $\sin \left( {{{\sin }^{ - 1}}\theta } \right) = \theta$ where $\theta$ is the angle.

Complete step by step answer:
This question is based on the inverse trigonometric function.
Consider the given question,
We have to find the value of \sqrt {1 + {x^2}} {\left[ {{{\left\\{ {x\cos \left( {{{\cot }^{ - 1}}x} \right) + \sin \left( {{{\cot }^{ - 1}}x} \right)} \right\\}}^2} - 1} \right]^{\dfrac{1}{2}}}
Let us consider the inverse trigonometric ratio $y = {\cot ^{ - 1}}x$,
now taking inverse , we have
This implies , $x = \cot y$
Now we find the value of $\sin y$ and $\cos y$
i.e. $\sin y = \dfrac{1}{{\sqrt {1 + {x^2}} }}$ and $\cos y = \dfrac{x}{{\sqrt {1 + {x^2}} }}$.
Taking inverse in both the values we get
$y = {\sin ^{ - 1}}\dfrac{1}{{\sqrt {1 + {x^2}} }}$ and $y = {\cos ^{ - 1}}\dfrac{x}{{\sqrt {1 + {x^2}} }}$
Thus, we have $y = {\cot ^{ - 1}}x = {\sin ^{ - 1}}\dfrac{1}{{\sqrt {1 + {x^2}} }} = {\cos ^{ - 1}}\dfrac{x}{{\sqrt {1 + {x^2}} }}$
Thus from the given question, we have,
\Rightarrow \sqrt {1 + {x^2}} {\left[ {{{\left\\{ {x\cos \left( {{{\cot }^{ - 1}}x} \right) + \sin \left( {{{\cot }^{ - 1}}x} \right)} \right\\}}^2} - 1} \right]^{\dfrac{1}{2}}}
Putting the value from above, we have
\Rightarrow \sqrt {1 + {x^2}} {\left[ {{{\left\\{ {x\cos \left( {{{\cos }^{ - 1}}\dfrac{x}{{\sqrt {1 + {x^2}} }}} \right) + \sin \left( {{{\sin }^{ - 1}}\dfrac{1}{{\sqrt {1 + {x^2}} }}} \right)} \right\\}}^2} - 1} \right]^{\dfrac{1}{2}}}
We know that $\cos \left( {{{\cos }^{ - 1}}\theta } \right) = \theta$ and $\sin \left( {{{\sin }^{ - 1}}\theta } \right) = \theta$,
Hence we have,
\Rightarrow \sqrt {1 + {x^2}} {\left[ {{{\left\\{ {x\dfrac{x}{{\sqrt {1 + {x^2}} }} + \dfrac{1}{{\sqrt {1 + {x^2}} }}} \right\\}}^2} - 1} \right]^{\dfrac{1}{2}}}
Taking LCM inside the curly bracket, we get
\Rightarrow \sqrt {1 + {x^2}} {\left[ {{{\left\\{ {\dfrac{{{x^2} + 1}}{{\sqrt {1 + {x^2}} }}} \right\\}}^2} - 1} \right]^{\dfrac{1}{2}}}
By cancelling on dividing $1 + {x^2}$ by $\sqrt {1 + {x^2}}$, we have
\Rightarrow \sqrt {1 + {x^2}} {\left[ {{{\left\\{ {\sqrt {1 + {x^2}} } \right\\}}^2} - 1} \right]^{\dfrac{1}{2}}}
On squaring we have,
$\Rightarrow \sqrt {1 + {x^2}} {\left[ {1 + {x^2} - 1} \right]^{\dfrac{1}{2}}}$
On simplifying we have,
$\Rightarrow \sqrt {1 + {x^2}} {\left[ {{x^2}} \right]^{\dfrac{1}{2}}}$
Hence on simplifying we have,
$\Rightarrow x\sqrt {1 + {x^2}}$
Hence, \sqrt {1 + {x^2}} {\left[ {{{\left\\{ {x\cos \left( {{{\cot }^{ - 1}}x} \right) + \sin \left( {{{\cot }^{ - 1}}x} \right)} \right\\}}^2} - 1} \right]^{\dfrac{1}{2}}} = x\sqrt {1 + {x^2}} . So, option $C$ is correct.

Note:
To find the value of inverse trigonometric ratio when value of one of the trigonometric ratio is given , we proceed as follow:
For example , we find the value of inverse other inverse trigonometric ratio , when we are given $\theta = {\cot ^{ - 1}}x$
This imply $x = \cot \theta$
We know that $\cot \theta = \dfrac{{base}}{{perpendicular}}$
Now from the right angle triangle , we have

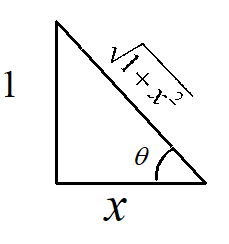
From Pythagoras theorem we have
$\text{hypotenuse} = \sqrt {1 + {x^2}}$
Hence, $\sin \theta = \dfrac{1}{{\sqrt {1 + {x^2}} }}$
Taking the inverse of the values we get .
Hence , $\theta = {\sin ^{ - 1}}\dfrac{1}{{\sqrt {1 + {x^2}} }}$ .
Similarly we can find the value of other inverse trigonometric ratios.