Question

If $(0,\beta )$lies on or inside the triangle with the sides $y+3x+2=0,3y-2x-5=0$ and $4y+x- 14=0$, then
(a) $0\le \beta \le \dfrac{7}{2}$
(b) $0\le \beta \le \dfrac{5}{2}$
(c) $\dfrac{5}{3}\le \beta \le \dfrac{7}{2}$
(d) None of these

Answer 1

Hint: Plot the given 3 line equations to form a triangle and find the point of intersection.

The figure for the given problem is as follows:

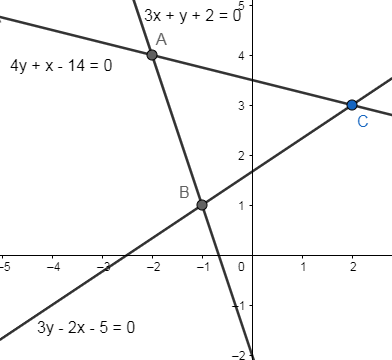
Now the given point $(0,\beta )$lies on the y-axis as its x-coordinate is zero.
From the above figure we see that the y-axis passes through the sides AC and BC.
Now we will substitute $(0,\beta )$ in the equation of side AC, i.e.,
$4y+x-14=0$
We get,
$4(\beta )+0-14=0$
$4\beta =14$
$\beta =\dfrac{14}{4}$
$\beta =\dfrac{7}{2}$
So the point of intersection of the y-axis and side AC is $\left( 0,\dfrac{7}{2} \right)$.
Similarly, we will substitute $(0,\beta )$ in the equation of side BC, i.e.,
$3y-2x-5=0$
We get,
$3\beta -2(0)-5=0$
$3\beta =5$
$\beta =\dfrac{5}{3}$
So, the point of intersection of the y-axis and side BC is $\left( 0,\dfrac{5}{3} \right)$.
Now as the given point lies on y-axis as well as on or inside of the triangle, so all the points between $\left( 0,\dfrac{5}{3} \right)$and $\left( 0,\dfrac{7}{2} \right)$, will satisfy the condition.
So, the value of $\beta$ will be,
$\dfrac{5}{3}\le \beta \le \dfrac{7}{2}$
Hence, the correct answer is option (c).
Note: Here we can solve for the vertices of the triangle from the given equations of the sides. Then find the value of $\beta$. But it will be a lengthy process.