Question
Question: The order of the differential equation of all circles whose radius is 4 is...
The order of the differential equation of all circles whose radius is 4 is
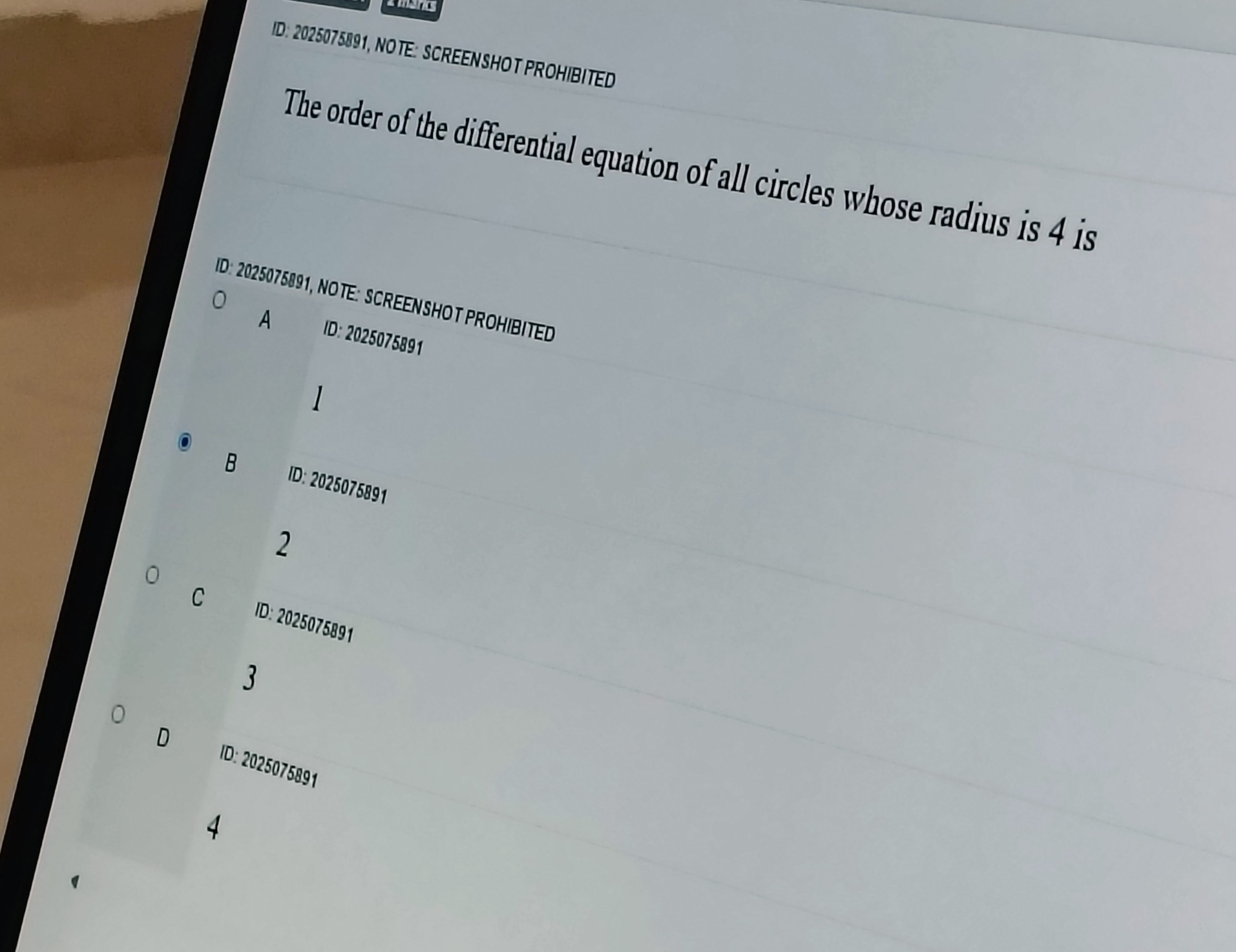
1
2
3
4
2
Solution
The general equation of a circle with center (h,k) and radius r is given by:
(x−h)2+(y−k)2=r2
In this problem, the radius is given as 4. So, the equation of the family of circles is:
(x−h)2+(y−k)2=42 (x−h)2+(y−k)2=16
To form a differential equation from a given family of curves, we need to eliminate the arbitrary constants present in the equation of the family. The order of the differential equation is equal to the number of independent arbitrary constants in the equation of the family of curves.
In the equation (x−h)2+(y−k)2=16, the arbitrary constants (parameters) are h and k. There are two independent arbitrary constants.
Therefore, the order of the differential equation for all circles whose radius is 4 will be 2.
