Question
Question: If the lines represented by equation $px^2$-$qy^2$=0 are distinct then...
If the lines represented by equation px2-qy2=0 are distinct then
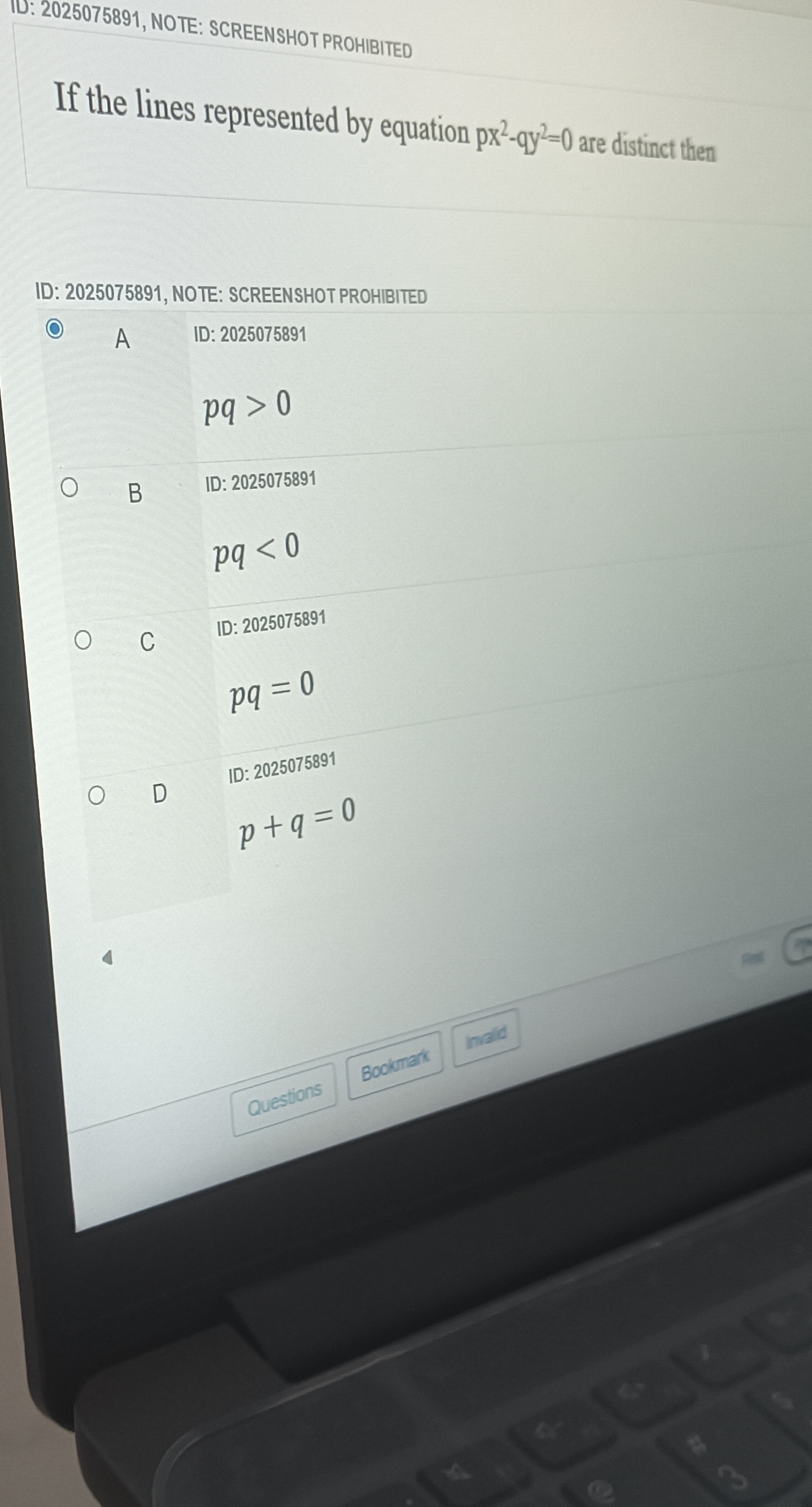
pq>0
pq<0
pq=0
p+q=0
A
Solution
The given equation is px2−qy2=0. This equation represents a pair of straight lines passing through the origin.
We can rewrite the equation as px2=qy2.
Case 1: If p=0 or q=0.
- If p=0, the equation becomes −qy2=0. If q=0, this simplifies to y2=0, which means y=0. This is the equation of the x-axis, a single line.
- If q=0, the equation becomes px2=0. If p=0, this simplifies to x2=0, which means x=0. This is the equation of the y-axis, a single line.
In both these scenarios (p=0 or q=0), the equation represents a single line, not two distinct lines. Therefore, for distinct lines, we must have p=0 and q=0.
Case 2: If p=0 and q=0.
We can write the equation as y2=qpx2.
Taking the square root on both sides, we get: y=±qpx
For these two lines to be real and distinct, the term under the square root, qp, must be a positive real number.
- If qp<0, then qp would be an imaginary number, meaning the lines would be imaginary (they would only intersect at the origin in the real plane).
- If qp=0, this would imply p=0 (since q=0), which we have already excluded as it leads to a single line.
Therefore, for two distinct real lines, we must have qp>0.
The condition qp>0 implies that p and q must have the same sign:
- If p>0 and q>0, then pq>0.
- If p<0 and q<0, then pq>0.
Thus, the condition for the lines to be distinct (real and distinct) is pq>0.
Alternative Method (Using General Equation of Pair of Straight Lines):
The general equation of a pair of straight lines passing through the origin is Ax2+2Hxy+By2=0.
The given equation is px2−qy2=0.
Comparing the coefficients:
A=p H=0 B=−q
For the lines to be real and distinct, the condition is H2−AB>0.
Substituting the values:
(0)2−(p)(−q)>0 0+pq>0 pq>0
Both methods yield the same result.
