Solveeit Logo
Login

Question

Question: If $A = \begin{bmatrix} x & 1 \\ 1 & 0 \end{bmatrix}$ and $A = A^{-1}$ then x =...

If A=[x110]A = \begin{bmatrix} x & 1 \\ 1 & 0 \end{bmatrix} and A=A−1A = A^{-1} then x =

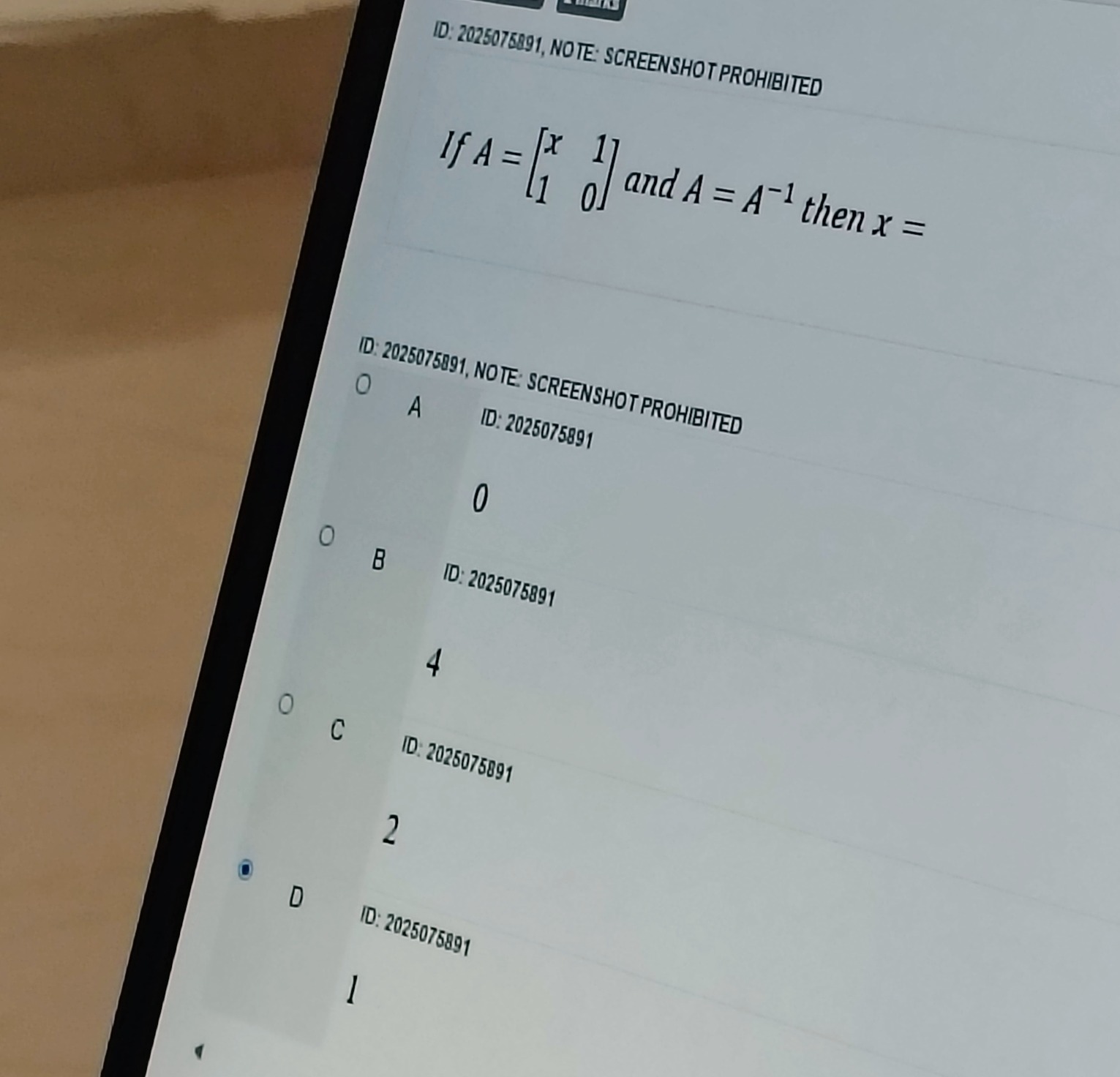
A

0

B

4

C

2

D

1

Answer

0

Explanation

Solution

The condition A=A−1A=A^{-1} implies A2=IA^2=I. Calculate A2A^2 by multiplying AA by itself. Equate the resulting matrix to the identity matrix II. Compare the corresponding elements of the matrices to form equations. Solve these equations for xx. All equations consistently yield x=0x=0.

Alternatively, we can calculate A−1A^{-1} directly. For a 2x2 matrix M=[abcd]M = \begin{bmatrix} a & b \\ c & d \end{bmatrix}, its inverse is M−1=1det⁡(M)[d−b−ca]M^{-1} = \frac{1}{\det(M)} \begin{bmatrix} d & -b \\ -c & a \end{bmatrix}. First, find the determinant of AA: det⁡(A)=(x)(0)−(1)(1)=0−1=−1\det(A) = (x)(0) - (1)(1) = 0 - 1 = -1.

Now, calculate A−1A^{-1}: A−1=1−1[0−1−1x]=[011−x]A^{-1} = \frac{1}{-1} \begin{bmatrix} 0 & -1 \\ -1 & x \end{bmatrix} = \begin{bmatrix} 0 & 1 \\ 1 & -x \end{bmatrix}.

Given A=A−1A = A^{-1}: [x110]=[011−x]\begin{bmatrix} x & 1 \\ 1 & 0 \end{bmatrix} = \begin{bmatrix} 0 & 1 \\ 1 & -x \end{bmatrix}

Comparing the corresponding elements: x=0x = 0