Question

A carnot engine, efficiency 30% and temperature of sink 300 K to increase efficiency up to 70% calculate change in temperature of source.

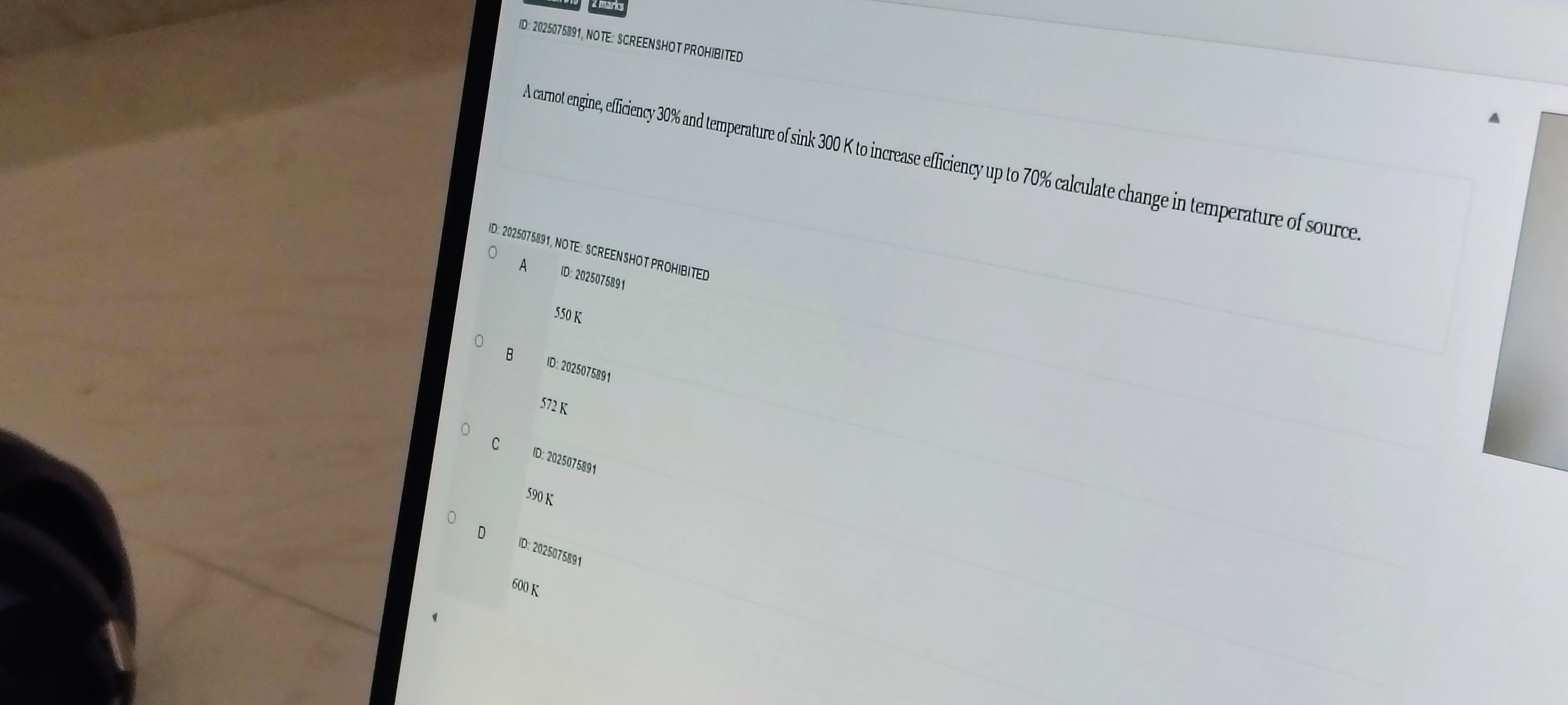
• A. 550 K
• B. 572 K
• C. 590 K
• D. 600 K

Answer 1

Answer: (B)

572 K

Answer 2

The efficiency of a Carnot engine is given by the formula:

$\eta = 1 - \frac{T_{sink}}{T_{source}}$

where $\eta$ is the efficiency, $T_{sink}$ is the temperature of the cold reservoir (sink), and $T_{source}$ is the temperature of the hot reservoir (source). All temperatures must be in Kelvin.

Given: Initial efficiency ($\eta_1$) = 30% = 0.30 Temperature of sink ($T_{sink}$) = 300 K

Step 1: Calculate the initial temperature of the source ($T_{source1}$) Using the efficiency formula for the initial state:

$0.30 = 1 - \frac{300}{T_{source1}}$

$\frac{300}{T_{source1}} = 1 - 0.30$

$\frac{300}{T_{source1}} = 0.70$

$T_{source1} = \frac{300}{0.70} = \frac{3000}{7} \, K$

Step 2: Calculate the final temperature of the source ($T_{source2}$) The efficiency is increased to 70% ($\eta_2$ = 0.70). The temperature of the sink remains constant at 300 K. Using the efficiency formula for the final state:

$0.70 = 1 - \frac{300}{T_{source2}}$

$\frac{300}{T_{source2}} = 1 - 0.70$

$\frac{300}{T_{source2}} = 0.30$

$T_{source2} = \frac{300}{0.30} = \frac{3000}{3} = 1000 \, K$

Step 3: Calculate the change in temperature of the source Change in temperature of source ($\Delta T_{source}$) = $T_{source2} - T_{source1}$

$\Delta T_{source} = 1000 - \frac{3000}{7}$

To subtract, find a common denominator:

$\Delta T_{source} = \frac{1000 \times 7}{7} - \frac{3000}{7}$

$\Delta T_{source} = \frac{7000 - 3000}{7}$

$\Delta T_{source} = \frac{4000}{7} \, K$

Now, convert the fraction to a decimal:

$\Delta T_{source} \approx 571.42857 \, K$

Comparing this value with the given options, the calculated value 571.42857 K is closest to 572 K.