Question

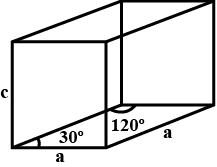
Ice crystallizes in a hexagonal lattice. At low temperature, at which the structure was determined, the lattice constants were $a=34\mathop A\limits^ \circ$ and $c=7.41\mathop A\limits^ \circ$. How many molecules of water are contained in a given unit cell? [Density of ice is $0.92{\text{ }}gc{m^{ - 3}}]$

Answer 1

Ice is water that has solidified into a crystal state. It may look translucent or more or less opaque bluish-white depending on the presence of impurities such as soil particles or air bubbles. One of the five two-dimensional Bravais lattice varieties is the hexagonal or triangular lattice. Wallpaper group p6m is the lattice's symmetry band. The hexagonal lattice's primitive translation vectors form a $120^o$ angle and are of similar length.

Complete answer:
The hexagonal crystal type of ordinary ice, or frozen water, is known as Ice Ih (hexagonal ice crystal) (pronounced: ice one h, also known as ice-phase-one). With the exception of a small volume of ice Ic that is rarely found in the upper atmosphere, almost all ice in the biosphere is ice Ih. Ice Ih has a number of unusual properties that are important for the survival of life and the control of global temperature.
The oxygen atoms form hexagonal symmetry with almost tetrahedral bonding angles in the crystal structure. X-ray diffraction and highly high precision thermal expansion tests show that ice Ih is stable down to $268{\text{ }}^\circ C{\text{ }}\left( {5{\text{ }}K;{\text{ }}450{\text{ }}^\circ F} \right)$. Ice Ih can also withstand pressures of up to 210 megapascals (2,100 atm) before transitioning to ice III or ice II.
Volume of unit cell, V= Area of Base × Height
=$2 \times \dfrac{{\sqrt 3 }}{4}{a^2} \times c$
$= 2 \times \dfrac{{\sqrt 3 }}{4} \times 1156 \times {10^{ - 16}} \times 7.41 \times {10^{ - 8}}\;{\text{c}}{{\text{m}}^3}$
The Mass of unit cell is given as = V × S
$= 7.409 \times {10^{ - 21}} \times 0.92$
$= 6.816 \times {10^{ - 21}}{\text{gm}}$
Let N be the water molecules in the given cell
$6.816 \times {10^{ - 21}} = {\text{n}} \times \dfrac{{18}}{{6.023 \times {{10}^{23}}}}$
n = 227.9
n = 228 molecules of Water

Note:
Linus Pauling suggested the agreed crystal structure of ordinary ice in 1935. Ice Ih has a composition that resembles crinkled planes made up of tessellating hexagonal rings with an oxygen atom at each vertex and hydrogen bonds forming the rings' edges. The planes alternate in an ABAB fashion, with B planes reflecting A planes along the same axes as the planes. Each bond has a distance between oxygen atoms of around 275 pm, which is the same distance between any two bound oxygen atoms in the lattice.