Question

$I(\alpha) = \int_0^1 \frac{x^\alpha - 1}{lnx}dx$

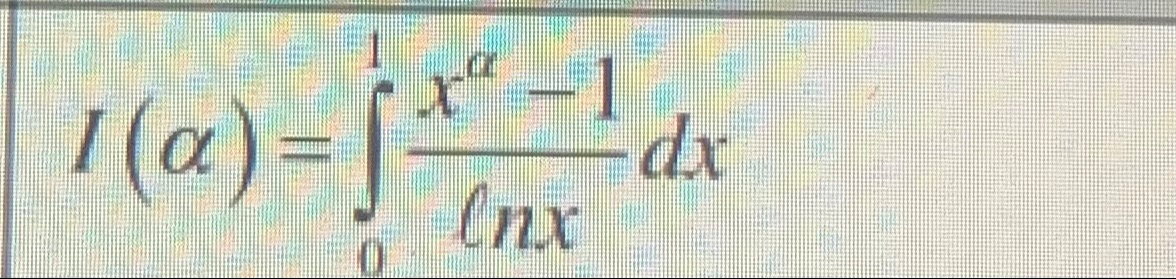
Answer 1

$I(\alpha)= \ln(\alpha+1)$

Answer 2

Solution:

Given

$$I(\alpha) = \int_0^1 \frac{x^\alpha - 1}{\ln x}\,dx.$$

1. Differentiate under the integral sign:
   Differentiate $I(\alpha)$ with respect to $\alpha$:

   $$I'(\alpha) = \frac{d}{d\alpha}\int_0^1 \frac{x^\alpha - 1}{\ln x}\,dx = \int_0^1 \frac{\partial}{\partial \alpha}\left(\frac{x^\alpha - 1}{\ln x}\right)dx.$$

2. Compute the derivative inside the integral:
   Since

   $$\frac{\partial}{\partial \alpha} x^\alpha = x^\alpha \ln x,$$

   we have:

   $$\frac{\partial}{\partial \alpha}\left(\frac{x^\alpha - 1}{\ln x}\right) = \frac{x^\alpha \ln x}{\ln x} = x^\alpha.$$

   Thus,

   $$I'(\alpha) = \int_0^1 x^\alpha\,dx.$$

3. Evaluate the resulting integral:

   $$\int_0^1 x^\alpha\,dx = \left[\frac{x^{\alpha+1}}{\alpha+1}\right]_0^1 = \frac{1}{\alpha+1}.$$

   So,

   $$I'(\alpha) = \frac{1}{\alpha+1}.$$

4. Integrate with respect to $\alpha$:

   $$I(\alpha) = \int \frac{1}{\alpha+1}\,d\alpha = \ln |\alpha+1| + C.$$

   Since $\alpha+1 > 0$, we have:

   $$I(\alpha) = \ln(\alpha+1) + C.$$

5. Determine the constant $C$:
   Evaluate at $\alpha=0$:

   $$I(0) = \int_0^1 \frac{1-1}{\ln x}\,dx = 0.$$

   Hence,

   $$0 = \ln(1) + C \quad \Rightarrow \quad C = 0.$$

Explanation of the Core Solution:
Differentiate under the integral sign to find $I'(\alpha)$ which simplifies to $\int_0^1 x^\alpha dx = \frac{1}{\alpha+1}$. Integrate back to get $I(\alpha)=\ln(\alpha+1) + C$ and use the condition $I(0)=0$ to find $C=0$.