Question
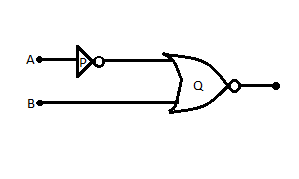
Question: (i) Write the truth table for logic gates marked \(P\) and \(Q\) in the given circuit. (ii) Write...
(i) Write the truth table for logic gates marked P and Q in the given circuit.
(ii) Write the truth table for the circuit.
Solution
The gate marked P is a NOT gate.
The gate marked Q is a NOR gate.
A when passed through NOT gate returns the inverted output.
When B and the output of A through NOT gate are passed through NOR gate, the output returned is high if and only if both the inputs are low.
Complete step by step solution:
(i) Gate marked P is a NOT GATE. It inverts the input and returns the value as output. Therefore, if the input is high, output is low and when input is low, output is high.
The logic equation of NOT gate is as follows:
Y=A
Where, Y is the output and A is the input.
Truth table of NOT GATE IS:
| INPUT( A ) | OUTPUT( Y ) |
|---|---|
| 1 | 0 |
| 0 | 1 |
The gate marked Q is a NOR gate. It gives a high output when both the inputs are low, and a low output when one or both the inputs are high.
The logic equation of NOR gate is as follows:
Y=A+B
Where, Y is the output while A and B are the input.
Truth table of NOR GATE IS:
| Input 1 ( A ) | Input 2 ( B ) | Y=A+B |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
(ii) The given circuit is a combinational circuit made out of basic logic gates:
The logic expression for the circuit is:
Y=A+B
Where, Y is the output while both A and B are inputs.
Truth table for NOR gate is:
| INPUT FOR P ( A ) | INPUT1 ( A ) | INPUT2 ( B ) | OUTPUT Y=A+B |
|---|---|---|---|
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 |
Note: NOT is a single input logic gate and is also known as the Inverter.
A NOR gate can have two or more inputs and is the result of negation of OR gate.
Remember that the final circuit takes inverted value of input A as its own input.
