Question

$\sin^2 A \cos^2 B + \cos^2 A \sin^2 B + \cos^2 A \cos^2 B + \sin^2 A \sin^2 B = 1$

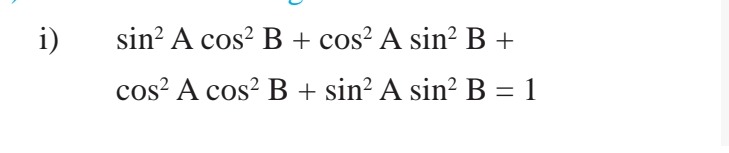
Answer 1

The given equation is an identity, true for all $A$ and $B$.

Answer 2

Solution Explanation:

Group the terms as follows:

$$\sin^2A\cos^2B + \sin^2A\sin^2B = \sin^2A (\cos^2B+\sin^2B) = \sin^2A(1)=\sin^2A$$ $$\cos^2A\sin^2B + \cos^2A\cos^2B = \cos^2A (\sin^2B+\cos^2B) = \cos^2A(1)=\cos^2A$$

Thus, the entire expression becomes:

$$\sin^2A + \cos^2A = 1$$

which is an identity valid for all values of $A$ and $B$.