Question

$I \le x:\frac{x}{I}+x = (x)f$

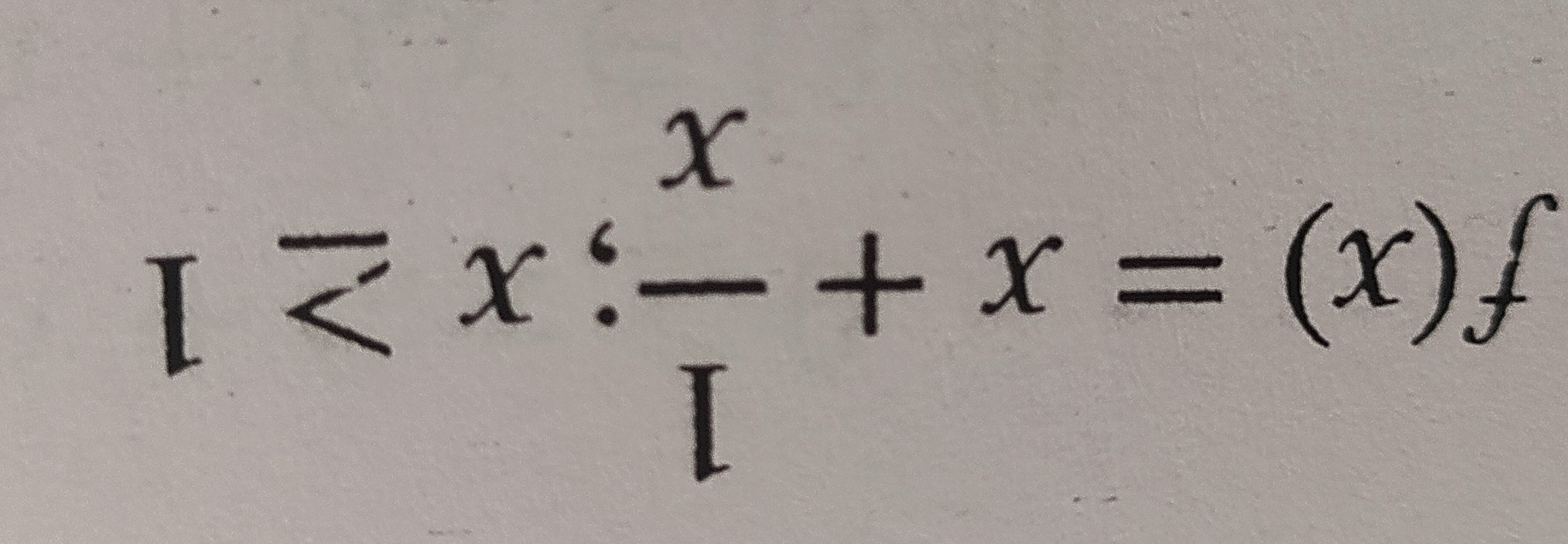
Answer 1

$f(x) = x \left(\frac{1+I}{I}\right)$ for $x \ge I$.

Answer 2

The given expression defines a function $f(x)$ for $x \ge I$ using the equation $\frac{x}{I} + x = f(x)$. By simplifying the right-hand side of the equation, we obtain the explicit form of the function $f(x)$. Factoring $x$ from the terms $\frac{x}{I}$ and $x$ gives $x(\frac{1}{I} + 1)$. Combining the terms inside the parenthesis leads to $x(\frac{1+I}{I})$. This expression defines $f(x)$ for the specified domain $x \ge I$.