Question

$\int_{0}^{2\pi} \left( \sum_{n=0}^{\infty} \frac{\cos(2^n x)}{2^n} \right)^2 dx$

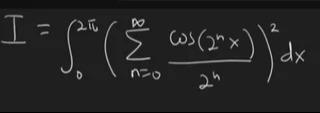
Answer 1

$\frac{4\pi}{3}$

Answer 2

The integral of the square of a uniformly convergent series can be computed by squaring the series term-by-term and then integrating term-by-term. The integral $\int_{0}^{2\pi} \cos(kx) \cos(mx) dx$ is zero if $k \ne m$ and $\pi$ if $k=m$ (for $k, m$ positive integers). Applying this to the squared series $\sum_{n,m} \frac{\cos(2^n x) \cos(2^m x)}{2^{n+m}}$, only terms where $n=m$ survive, leading to $\sum_{n=0}^{\infty} \frac{\pi}{2^{2n}}$. This sum is a geometric series $\pi \sum_{n=0}^{\infty} (1/4)^n = \pi/(1-1/4) = 4\pi/3$.