Question

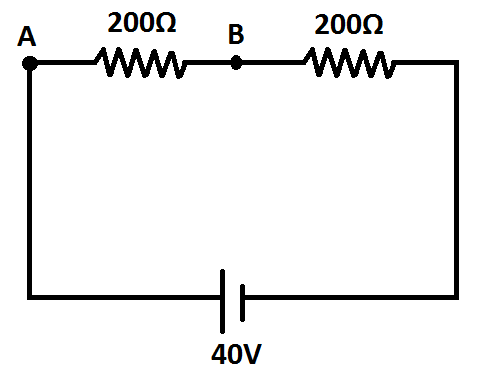
(i) In fig. find the potential difference between point A and B.
(ii) Now we wish to measure this potential difference by using a voltmeter of resistance $2k\Omega$ . Find the reading of the voltmeter and percentage error.
(iii) Solve part (ii) if the voltmeter were of resistance $20k\Omega$ .
What conclusion do you draw from the results you get in the above parts?

Answer 1

Hint : Here, to solve the first question we have to consider the fact that both the resistances are connected in series, and therefore the voltage will be divided in both. For the second and the third question, first we have to find the equivalent resistance of the resistor and the resistance of the voltmeter. After that, we will find the potential difference between A and B in this particular case and then find the percentage error.

Complete Step By Step Answer:
Answer (i): We can see here that both the resistances are the same, the voltage of $40V$ will be divided equally among both these resistances. Therefore, we can say that the potential difference across A and B is $20V$ .
Answer (ii): Let us first consider the diagram for the given condition.

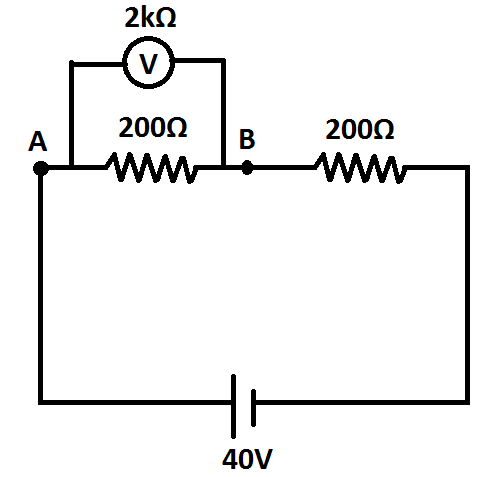
Here, the equivalent resistance of $200\Omega$ and $2k\Omega$ is given by:
$R = \dfrac{{200 \times 2000}}{{200 + 2000}} = \dfrac{{2000}}{{11}}\Omega$
The voltmeter will show the reading similar to the potential difference between A and B ${V_{AB}}$ .
${V_{AB}} = 40 \times \dfrac{{\dfrac{{2000}}{{11}}}}{{\dfrac{{2000}}{{11}} + 200}} = 40 \times \dfrac{{\dfrac{{2000}}{{11}}}}{{\dfrac{{4400}}{{11}}}} = 40 \times \dfrac{{20}}{{44}} = 18.18V$
Therefore, the percentage error $= \dfrac{{20 - 18.18}}{{20}} \times 100 = 9.1\%$ .
Answer (iii): Let us first consider the diagram for the given condition.

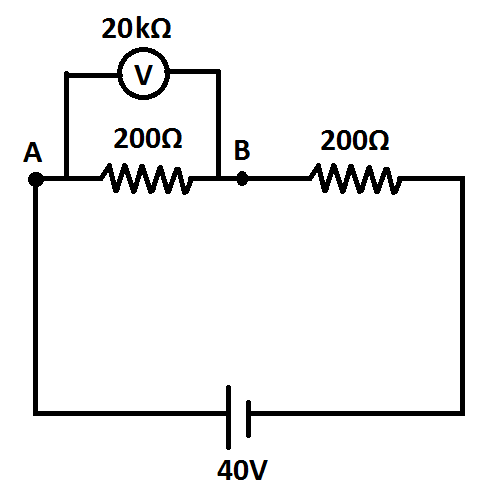
Here, the equivalent resistance of $200\Omega$ and $20k\Omega$ is given by:
$R = \dfrac{{200 \times 20000}}{{200 + 20000}} = \dfrac{{20000}}{{101}}\Omega$
The voltmeter will show the reading similar to the potential difference between A and B ${V_{AB}}$ .
${V_{AB}} = 40 \times \dfrac{{\dfrac{{20000}}{{101}}}}{{\dfrac{{20000}}{{101}} + 200}} = 40 \times \dfrac{{\dfrac{{20000}}{{101}}}}{{\dfrac{{40200}}{{101}}}} = 40 \times \dfrac{{200}}{{402}} = 19.90V$
Therefore, the percentage error $= \dfrac{{20 - 19.90}}{{20}} \times 100 = 0.5\%$ .

Note :
We can observe here that the voltmeter resistance is greater in the third case than that of the second case. As a result, the percentage error in the potential difference is lesser in the third case than that of the second case. Thus, we can conclude that as the voltmeter resistance increases, the percentage error decreases.