Question
Question: (i) $\frac{2^{x^2}}{2^{2x}}=\frac{8^x}{64}$...
(i) 22x2x2=648x
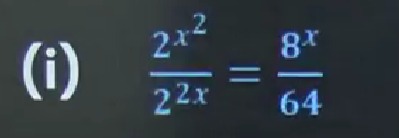
x=2, 3
Solution
To solve the equation 22x2x2=648x, we will use the properties of exponents to simplify both sides of the equation to the same base.
Step 1: Express all terms with the same base (base 2). We know that 8=23 and 64=26.
The left side of the equation is: 22x2x2 Using the exponent property anam=am−n, we get: 2x2−2x
The right side of the equation is: 648x Substitute 8=23 and 64=26: 26(23)x Using the exponent property (am)n=amn, we get: 2623x Now, using the exponent property anam=am−n, we get: 23x−6
Step 2: Equate the simplified expressions. Now the equation becomes: 2x2−2x=23x−6
Step 3: Equate the exponents. Since the bases are the same (both are 2), the exponents must be equal: x2−2x=3x−6
Step 4: Rearrange into a standard quadratic equation. Move all terms to one side to form a quadratic equation ax2+bx+c=0: x2−2x−3x+6=0 x2−5x+6=0
Step 5: Solve the quadratic equation. We can solve this quadratic equation by factoring. We need two numbers that multiply to 6 and add up to -5. These numbers are -2 and -3. So, the equation can be factored as: (x−2)(x−3)=0
This gives two possible solutions for x: x−2=0⟹x=2 x−3=0⟹x=3
Step 6: Verify the solutions (optional but recommended). For x=2: LHS: 22×2222=2424=1 RHS: 6482=6464=1 LHS = RHS, so x=2 is a solution.
For x=3: LHS: 22×3232=2629=29−6=23=8 RHS: 6483=64512=8 LHS = RHS, so x=3 is a solution.
Both solutions are valid.
The final answer is x=2,3.
Explanation of the solution: The given exponential equation is simplified by expressing all terms with the same base (base 2). Using exponent properties am/an=am−n and (am)n=amn, the equation transforms into 2x2−2x=23x−6. Equating the exponents yields a quadratic equation x2−2x=3x−6, which simplifies to x2−5x+6=0. Factoring this quadratic equation gives (x−2)(x−3)=0, leading to the solutions x=2 and x=3.
