Question

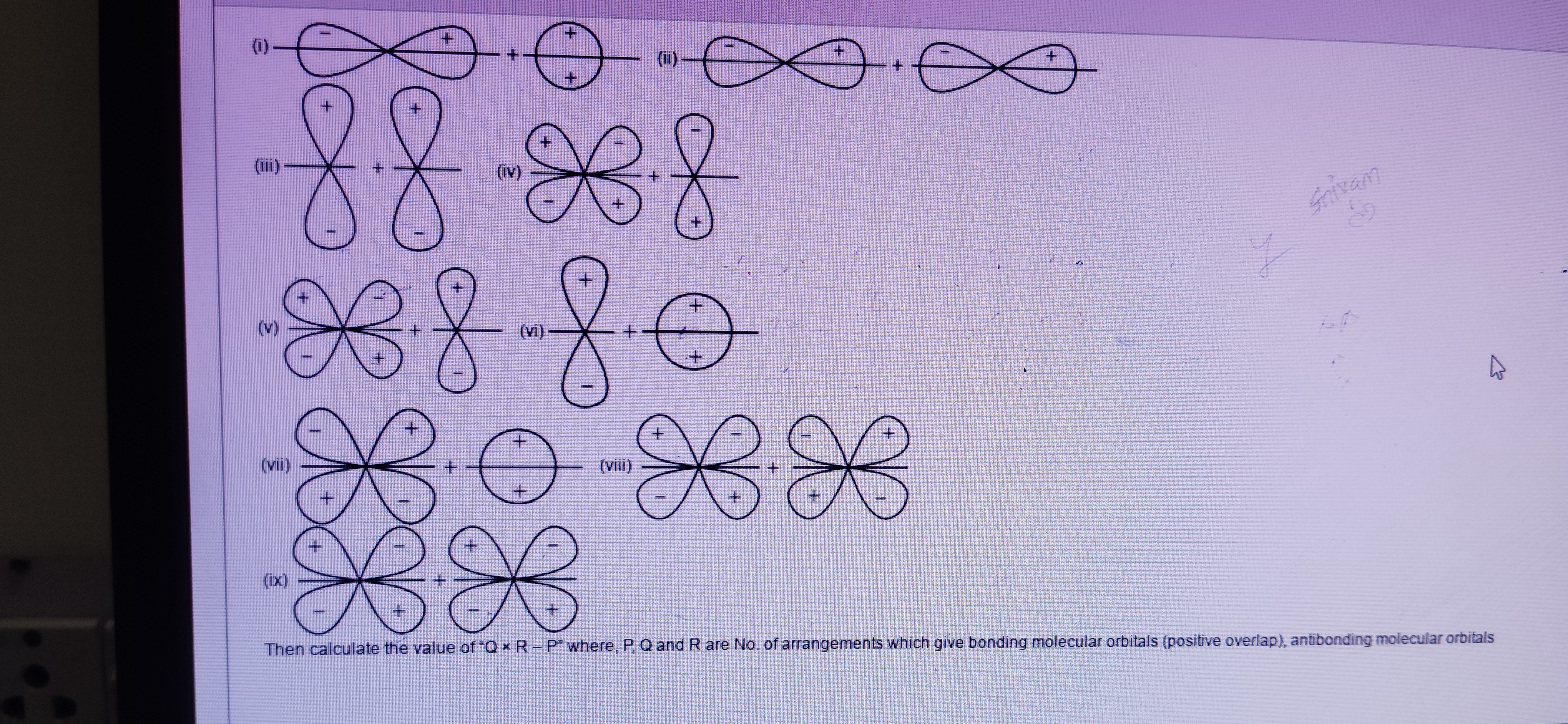
(i)

(ii)

(iii)

(iv)

(v)

(vi)

(vii)

(viii)

(ix)

Then calculate the value of "Q x R - P" where, P, Q and R are No. of arrangements which give bonding molecular orbitals (positive overlap), antibonding molecular orbitals

Answer 1

2

Answer 2

The types of overlaps in each diagram are analyzed as follows:

(i) Overlap of a p-orbital (perpendicular to the internuclear axis) and an s-orbital. This is a non-bonding interaction due to cancellation of positive and negative overlaps by symmetry.

(ii) Sideways overlap of two p-orbitals with opposite phases overlapping. This is an antibonding $\pi^*$ interaction.

(iii) Head-on overlap of two p-orbitals with the same phase overlapping. This is a bonding $\sigma$ interaction.

(iv) Overlap of a d-orbital and a p-orbital. Due to symmetry, the net overlap is zero, resulting in a non-bonding interaction.

(v) Overlap of two d-orbitals resulting in a bonding $\delta$ interaction.

(vi) Overlap of a p-orbital (along the internuclear axis) and an s-orbital. This is a non-bonding interaction due to cancellation of positive and negative overlaps by symmetry.

(vii) Overlap of a d-orbital and an s-orbital. Due to symmetry, the net overlap is zero, resulting in a non-bonding interaction.

(viii) Sideways overlap of two p-orbitals with the same phase overlapping. This is a bonding $\pi$ interaction.

(ix) Overlap of two d-orbitals resulting in an antibonding $\delta^*$ interaction.

Based on the analysis:

• Number of bonding molecular orbitals (positive overlap), Q = 3 (from iii, v, viii)
• Number of antibonding molecular orbitals (negative overlap), R = 2 (from ii, ix)
• Number of non-bonding interactions, P = 4 (from i, iv, vi, vii)

We need to calculate the value of $Q \times R - P$.

$Q \times R - P = 3 \times 2 - 4 = 6 - 4 = 2$.