Question

(i) Calculate the work done when $F=\left( 5\hat{i}+3\hat{j}+2\hat{k} \right)N$ and $S=\left( 3\hat{i}-\hat{j}+2\hat{k} \right)m$ acting in the same direction.
(ii) Show with the help of a vector diagram that the work-done is a scalar product of force and displacement.

Answer 1

A scalar product can be defined as the product of two vector quantities which results in a scalar. Force is a vector quantity and displacement is also a vector quantity. Work done can be defined as the dot product or scalar product of the force and the displacement.

Complete step-by-step solution
The force on the object is given as, $F=\left( 5\hat{i}+3\hat{j}+2\hat{k} \right)N$
The distance covered by the object is, $S=\left( 3\hat{i}-\hat{j}+2\hat{k} \right)m$
The work done on an object on which a force is acting and moves by a distance can be given by the dot product of the force and the distance. Simply, we can define that work done by a force can be defined as the product of the force in the direction of movement of the object and the distance covered by the object.
Work done is,
$\begin{aligned} &\Rightarrow W=\vec{F}.\vec{S}=\left( 5\hat{i}+3\hat{j}+2\hat{k} \right).\left( 3\hat{i}-\hat{j}+2\hat{k} \right) \\\ & \Rightarrow W=15-3+4 \\\ & \Rightarrow W=16J \\\ \end{aligned}$
So, the work done is 16 joules. The force and the displacement are vector quantities, while the work done is a scalar quantity.

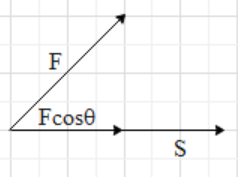
Find the component of the force F in the direction of the displacement. The component of the force is $F\cos \theta$, where $\theta$ is the angle between the force and the displacement. Then multiply the component of a force and the displacement to find the work done.
$W=FS\cos \theta$

Note: A scalar quantity can be defined as a quantity which has only magnitude, not direction. A vector quantity can be defined as the quantity which has both the direction and the magnitude. We have the force and displacement as a vector quantity. But the work done found from the force and the displacement is a scalar quantity.