Question

Hydrogen atoms in ground state are excited by monochromatic radiation $\lambda = 975A^\circ$. How many numbers of spectral lines will be emitted in the resulting spectrum?
A. $3$
B. $2$
C. $6$
D. $10$

Answer 1

Energy of incident radiation, $E = \dfrac{{hc}}{\lambda }$
$h = 6.62607015 \times {10^ - }^{34}\;{\text{Joule s}}$, is Planck's constant.
$c = 3 \times {10^8}\;{\text{m/s}}$, is the speed of light.
Number of spectral line, ${N_E} = \;\dfrac{{n\left( {n - 1} \right)}}{2}$

Complete step by step solution:
The smallest atoms are hydrogen, which comprises only an electron and a proton. The ground hydrogen state is the lowest allowable energy level and has zero angular momentum. It is therefore the most stable state in which the 1s atomic orbital was filled by a single electron.

Given, radiation, $\lambda = 975A^\circ$,
Where, $\lambda$ is the wavelength.
Convert the wavelength into ${\text{nm}}$.
Therefore, $\lambda = 97.5\;{\text{nm}}$

We know that, energy of incident radiation, $E = \dfrac{{hc}}{\lambda }$ …… (i)

Where, $h = 6.62607015 \times {10^ - }^{34}\;{\text{joule second}}$, is Planck's constant.
$c = 3 \times {10^8}\;{\text{m/s}}$, is the speed of light.

Now, place the values of $h$,$c$, and $\lambda$ in equation (i)
Therefore,

$$E = \dfrac{{hc}}{\lambda } \\\ = \dfrac{{6.63 \times {{10}^{ - 34}} \times 3 \times {{10}^8}}}{{97.5 \times {{10}^{ - 9}}}}\;{\text{J}} \\\$$

The energy found above is in joules, but it needs to be converted into electron volt.
We know:
$1\,{\text{eV = 1}}{\text{.602}} \times {\text{1}}{{\text{0}}^{ - {\text{19}}}}{\text{J}}$
So, to convert the energy into electron volt, divide the energy in joules by ${\text{1}}{\text{.602}} \times {\text{1}}{{\text{0}}^{ - {\text{19}}}}{\text{J}}$.

Therefore,

$$E = \dfrac{{hc}}{\lambda } \\\ = \dfrac{{6.63 \times {{10}^{ - 34}} \times 3 \times {{10}^8}}}{{97.5 \times {{10}^{ - 9}} \times 1.602 \times {{10}^{ - 9}}}}\;{\text{eV}} \\\ = {\text{12}}{\text{.75}}\;{\text{eV}} \\\$$

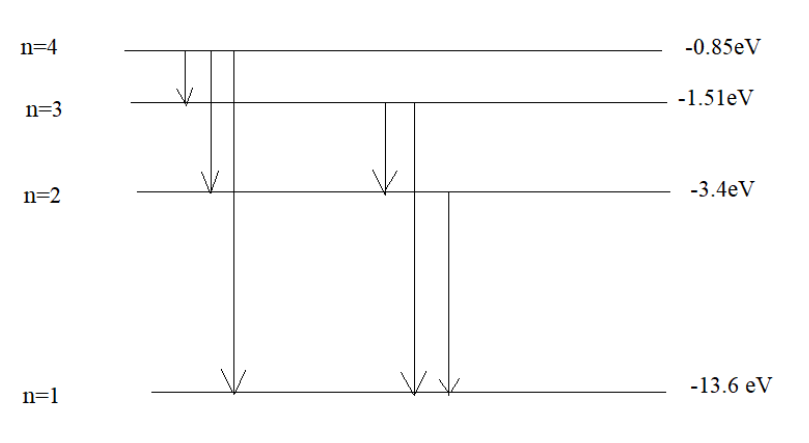
The energy associated with the base state is $- 13.6\;{\text{eV}}$, energy associated to the first excited state is $- 3.4\;{\text{eV}}$, energy associated to the second excited state is $- 1.51\;{\text{eV}}$and energy associated to the third excited state is $- 0.85\;{\text{eV}}$.
After it has absorbed a photon of energy ${\text{12}}{\text{.75}}\;{\text{eV}}$, the electron will reach to third excited state of energy $- {\text{0}}{\text{.85}}\;{\text{eV}}$, which can be illustrated by the simple calculation given below:
Energy difference:

$$\Delta E = \left( { - 13.6 + 12.75} \right)\,{\text{ eV}} \\\ {\text{ = }} - 0.85\,{\text{eV}} \\\$$

Hence, the energy newly found corresponds to the third excited state where $n = 4$.
Since, energy difference corresponding to
$n = 1$ and $n = 4$ is $12.75\;{\text{eV}}$

Now, number of lines will be,
${N_E} = \;\dfrac{{n\left( {n - 1} \right)}}{2}$ …… (i)
Place the value of $n = 4$ in equation (i)

Therefore,
${N_E} = \;\dfrac{{4 \times \left( {4 - 1} \right)}}{2} \\\ = \dfrac{{4 \times 3}}{2} \\\ = 6 \\\$

**Hence, the number of spectral lines that will be emitted is $6$.

Hence, the correct answer is C.**

Note: In this problem, you are asked to find the number of spectral lines emitted. So, to find this, first find the energy absorbed by the atom by the mentioned wavelength. It should be converted into electron volts associated with the energy found. Always add the energy absorbed to the base energy. Subtracting the energy absorbed will definitely affect the result. Find the excited level by the energy associated with various energy levels.