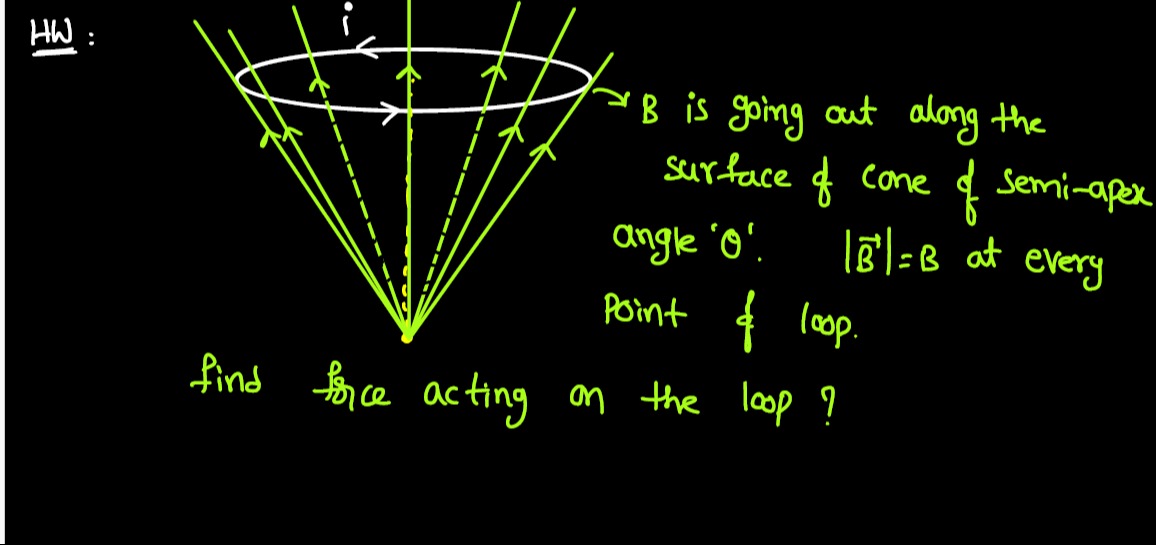
Question

B is going out along the surface of cone of semi-apex angle '$\theta$'. $|\overrightarrow{B}|$ = B at every point of loop. find force acting on the loop?

• A. The force is zero due to symmetry.
• B. $2\pi I r B \cos\theta$ along the axis of the cone.
• C. $2\pi I r B \sin\theta$ along the axis of the cone.
• D. $2\pi I r B$ perpendicular to the axis of the cone.

Answer 1

Answer: (C)

The force acting on the loop is $2\pi I r B \sin\theta$ directed along the axis of the cone, away from the apex.

Answer 2

The force on a current-carrying loop in a magnetic field is given by \vec{F} = \oint I d\vec{l} \times \vec{B}}. The magnetic field $\vec{B}$ is along the surface of the cone, pointing radially outwards from the apex. The magnitude of $\vec{B}$ is $B$ and the semi-apex angle of the cone is $\theta$. The loop is a circle of radius $r$ lying on the surface of the cone, perpendicular to the cone's axis. The current $i$ flows in a circular direction around the loop.

We can decompose the magnetic field $\vec{B}$ into two components:

1. A component perpendicular to the plane of the loop: $\vec{B}_{\perp}$. This component is along the axis of the cone. Since the slant height makes an angle $\theta$ with the axis, $\vec{B}_{\perp} = B \cos\theta \hat{k}$ (assuming the loop is in the xy-plane and the cone axis is along the z-axis).
2. A component parallel to the plane of the loop: $\vec{B}_{\parallel}$. This component lies in the radial direction within the plane of the loop. Its magnitude is $B \sin\theta$, so $\vec{B}_{\parallel} = B \sin\theta \hat{r}$, where $\hat{r}$ is the radial unit vector in the plane of the loop.

The force on the loop is $\vec{F} = \oint I d\vec{l} \times (\vec{B}_{\perp} + \vec{B}_{\parallel}) = \oint I d\vec{l} \times \vec{B}_{\perp} + \oint I d\vec{l} \times \vec{B}_{\parallel}$.

The first term, $\oint I d\vec{l} \times \vec{B}_{\perp}$: $d\vec{l}$ is tangential to the loop. $\vec{B}_{\perp}$ is along the z-axis. The cross product $d\vec{l} \times \hat{k}$ results in a radial vector in the xy-plane. When integrated over the entire circular loop, the net force due to this component is zero due to symmetry. Alternatively, integrating $d\vec{l} \times \hat{k}$ over the loop gives zero.

The second term, $\oint I d\vec{l} \times \vec{B}_{\parallel}$: $d\vec{l}$ is tangential to the loop, and $\vec{B}_{\parallel}$ is radial in the plane of the loop. Let the loop be in the xy-plane. $d\vec{l} = r d\phi \hat{\phi}$ (where $\hat{\phi}$ is the tangential unit vector) and $\vec{B}_{\parallel} = B \sin\theta \hat{r}$. The cross product $d\vec{l} \times \vec{B}_{\parallel} = (r d\phi \hat{\phi}) \times (B \sin\theta \hat{r}) = r B \sin\theta d\phi (\hat{\phi} \times \hat{r})$. The cross product $\hat{\phi} \times \hat{r}$ is the unit vector perpendicular to the plane of the loop, which is $\hat{k}$ (if the current is counter-clockwise as shown in the figure). So, $d\vec{l} \times \vec{B}_{\parallel} = r B \sin\theta d\phi \hat{k}$. Integrating over the loop (from $\phi=0$ to $2\pi$): $\vec{F}_{\parallel} = \oint I d\vec{l} \times \vec{B}_{\parallel} = \int_0^{2\pi} I (r B \sin\theta d\phi \hat{k}) = I r B \sin\theta \hat{k} \int_0^{2\pi} d\phi = I r B \sin\theta (2\pi) \hat{k}$. The total force is $\vec{F} = \vec{F}_{\perp} + \vec{F}_{\parallel} = 0 + 2\pi I r B \sin\theta \hat{k}$.

The force is directed upwards, along the axis of the cone. The magnitude of the force is $2\pi I r B \sin\theta$.

The force acting on the loop is $2\pi I r B \sin\theta$ directed along the axis of the cone, away from the apex.