Solveeit Logo
Login

Question

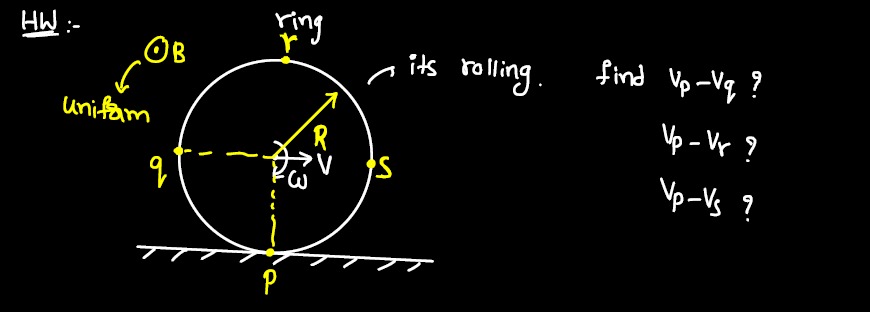
Question: HW:- ring its rolling. find $V_p - V_q$ ? $V_p - V_r$ ? $V_p - V_s$ ?...

HW:-

ring its rolling. find Vp−VqV_p - V_q ? Vp−VrV_p - V_r ? Vp−VsV_p - V_s ?

Answer

Vp−Vq=BVR,Vp−Vr=2BVR,Vp−Vs=BVRV_p - V_q = BVR, V_p - V_r = 2BVR, V_p - V_s = BVR

Explanation

Solution

The problem asks for the potential difference between various points on a rolling ring in a uniform magnetic field. The ring is rolling without slipping.

Let R be the radius of the ring. Let V be the velocity of the center of the ring to the right. Let ω\omega be the angular velocity of the ring (clockwise). The magnetic field B⃗\vec{B} is uniform and points out of the page, so B⃗=Bk^\vec{B} = B\hat{k}.

1. Rolling without slipping condition:

For rolling without slipping, the velocity of the point of contact (P) with the ground is zero. Let the center of the ring be C. The velocity of the center is V⃗C=Vi^\vec{V}_C = V\hat{i}. The angular velocity is ω⃗=−ωk^\vec{\omega} = -\omega\hat{k} (clockwise). The velocity of any point on the ring is given by v⃗=V⃗C+ω⃗×r⃗\vec{v} = \vec{V}_C + \vec{\omega} \times \vec{r}, where r⃗\vec{r} is the position vector of the point relative to the center C.

For point P, r⃗CP=−Rj^\vec{r}_{CP} = -R\hat{j}. v⃗P=Vi^+(−ωk^)×(−Rj^)=Vi^+ωR(k^×j^)=Vi^+ωR(−i^)=(V−ωR)i^\vec{v}_P = V\hat{i} + (-\omega\hat{k}) \times (-R\hat{j}) = V\hat{i} + \omega R (\hat{k} \times \hat{j}) = V\hat{i} + \omega R (-\hat{i}) = (V - \omega R)\hat{i}. Since v⃗P=0\vec{v}_P = 0, we have V−ωR=0  ⟹  V=ωRV - \omega R = 0 \implies V = \omega R.

2. Velocities of the points P, Q, R, S:

Using V=ωRV = \omega R:

  • Point P (bottom): r⃗CP=−Rj^\vec{r}_{CP} = -R\hat{j} v⃗P=(V−ωR)i^=0\vec{v}_P = (V - \omega R)\hat{i} = 0.
  • Point Q (left): r⃗CQ=−Ri^\vec{r}_{CQ} = -R\hat{i} v⃗Q=Vi^+(−ωk^)×(−Ri^)=Vi^+ωR(k^×i^)=Vi^+ωRj^=Vi^+Vj^\vec{v}_Q = V\hat{i} + (-\omega\hat{k}) \times (-R\hat{i}) = V\hat{i} + \omega R (\hat{k} \times \hat{i}) = V\hat{i} + \omega R \hat{j} = V\hat{i} + V\hat{j}.
  • Point R (top): r⃗CR=Rj^\vec{r}_{CR} = R\hat{j} v⃗R=Vi^+(−ωk^)×(Rj^)=Vi^−ωR(k^×j^)=Vi^−ωR(−i^)=(V+ωR)i^=2Vi^\vec{v}_R = V\hat{i} + (-\omega\hat{k}) \times (R\hat{j}) = V\hat{i} - \omega R (\hat{k} \times \hat{j}) = V\hat{i} - \omega R (-\hat{i}) = (V + \omega R)\hat{i} = 2V\hat{i}.
  • Point S (right): r⃗CS=Ri^\vec{r}_{CS} = R\hat{i} v⃗S=Vi^+(−ωk^)×(Ri^)=Vi^−ωR(k^×i^)=Vi^−ωRj^=Vi^−Vj^\vec{v}_S = V\hat{i} + (-\omega\hat{k}) \times (R\hat{i}) = V\hat{i} - \omega R (\hat{k} \times \hat{i}) = V\hat{i} - \omega R \hat{j} = V\hat{i} - V\hat{j}.

3. Potential difference formula:

The potential difference between two points A and B on a conductor moving in a magnetic field is given by: VA−VB=∫BA(v⃗×B⃗)⋅dl⃗V_A - V_B = \int_B^A (\vec{v} \times \vec{B}) \cdot d\vec{l} where v⃗\vec{v} is the velocity of the conductor element dl⃗d\vec{l}.

Let's calculate v⃗×B⃗\vec{v} \times \vec{B} for a general point on the ring. Let the center of the ring be C. The position of a point on the ring relative to C is r⃗=xi^+yj^\vec{r} = x\hat{i} + y\hat{j}. The velocity of this point is v⃗=V⃗C+ω⃗×r⃗=Vi^+(−ωk^)×(xi^+yj^)=Vi^−ωx(k^×i^)−ωy(k^×j^)\vec{v} = \vec{V}_C + \vec{\omega} \times \vec{r} = V\hat{i} + (-\omega\hat{k}) \times (x\hat{i} + y\hat{j}) = V\hat{i} - \omega x(\hat{k} \times \hat{i}) - \omega y(\hat{k} \times \hat{j}) v⃗=Vi^−ωxj^+ωyi^=(V+ωy)i^−ωxj^\vec{v} = V\hat{i} - \omega x\hat{j} + \omega y\hat{i} = (V + \omega y)\hat{i} - \omega x\hat{j}. Now, v⃗×B⃗=((V+ωy)i^−ωxj^)×(Bk^)\vec{v} \times \vec{B} = ((V + \omega y)\hat{i} - \omega x\hat{j}) \times (B\hat{k}) v⃗×B⃗=B(V+ωy)(i^×k^)−Bωx(j^×k^)\vec{v} \times \vec{B} = B(V + \omega y)(\hat{i} \times \hat{k}) - B\omega x(\hat{j} \times \hat{k}) v⃗×B⃗=B(V+ωy)(−j^)−Bωx(i^)\vec{v} \times \vec{B} = B(V + \omega y)(-\hat{j}) - B\omega x(\hat{i}) v⃗×B⃗=−Bωxi^−B(V+ωy)j^\vec{v} \times \vec{B} = -B\omega x\hat{i} - B(V + \omega y)\hat{j}. Since V=ωRV = \omega R, we have: v⃗×B⃗=−Bωxi^−B(ωR+ωy)j^=−Bωxi^−Bω(R+y)j^\vec{v} \times \vec{B} = -B\omega x\hat{i} - B(\omega R + \omega y)\hat{j} = -B\omega x\hat{i} - B\omega(R + y)\hat{j}.

4. Calculation of potential differences:

  • VP−VQV_P - V_Q: We integrate from Q to P. The path from Q to P is along the circumference. However, we can choose a simpler path, for example, from Q to C and then from C to P. VP−VQ=(VP−VC)+(VC−VQ)V_P - V_Q = (V_P - V_C) + (V_C - V_Q). Let's calculate VP−VCV_P - V_C and VC−VQV_C - V_Q. Path from C to P: r⃗CP=−Rj^\vec{r}_{CP} = -R\hat{j}. dl⃗=dyj^d\vec{l} = dy\hat{j} from y=0y=0 to y=−Ry=-R. VP−VC=∫CP(v⃗×B⃗)⋅dl⃗=∫0−R(−Bωxi^−Bω(R+y)j^)⋅(dyj^)V_P - V_C = \int_C^P (\vec{v} \times \vec{B}) \cdot d\vec{l} = \int_0^{-R} (-B\omega x\hat{i} - B\omega(R + y)\hat{j}) \cdot (dy\hat{j}). Along the path from C to P, x=0x=0. VP−VC=∫0−R(−Bω(R+y)j^)⋅(dyj^)=∫0−R−Bω(R+y)dyV_P - V_C = \int_0^{-R} (-B\omega(R + y)\hat{j}) \cdot (dy\hat{j}) = \int_0^{-R} -B\omega(R + y) dy VP−VC=−Bω[Ry+y22]0−R=−Bω[R(−R)+(−R)22]=−Bω[−R2+R22]=−Bω(−R22)=12BωR2V_P - V_C = -B\omega \left[ Ry + \frac{y^2}{2} \right]_0^{-R} = -B\omega \left[ R(-R) + \frac{(-R)^2}{2} \right] = -B\omega \left[ -R^2 + \frac{R^2}{2} \right] = -B\omega \left( -\frac{R^2}{2} \right) = \frac{1}{2}B\omega R^2. Path from Q to C: r⃗CQ=−Ri^\vec{r}_{CQ} = -R\hat{i}. dl⃗=dxi^d\vec{l} = dx\hat{i} from x=−Rx=-R to x=0x=0. VC−VQ=∫QC(v⃗×B⃗)⋅dl⃗=∫−R0(−Bωxi^−Bω(R+y)j^)⋅(dxi^)V_C - V_Q = \int_Q^C (\vec{v} \times \vec{B}) \cdot d\vec{l} = \int_{-R}^0 (-B\omega x\hat{i} - B\omega(R + y)\hat{j}) \cdot (dx\hat{i}). Along the path from Q to C, y=0y=0. VC−VQ=∫−R0(−Bωxi^)⋅(dxi^)=∫−R0−BωxdxV_C - V_Q = \int_{-R}^0 (-B\omega x\hat{i}) \cdot (dx\hat{i}) = \int_{-R}^0 -B\omega x dx VC−VQ=−Bω[x22]−R0=−Bω[0−(−R)22]=−Bω(−R22)=12BωR2V_C - V_Q = -B\omega \left[ \frac{x^2}{2} \right]_{-R}^0 = -B\omega \left[ 0 - \frac{(-R)^2}{2} \right] = -B\omega \left( -\frac{R^2}{2} \right) = \frac{1}{2}B\omega R^2. Therefore, VP−VQ=(VP−VC)+(VC−VQ)=12BωR2+12BωR2=BωR2V_P - V_Q = (V_P - V_C) + (V_C - V_Q) = \frac{1}{2}B\omega R^2 + \frac{1}{2}B\omega R^2 = B\omega R^2. Since V=ωRV = \omega R, VP−VQ=BVRV_P - V_Q = BVR.

  • VP−VRV_P - V_R: We integrate from R to P. Path from R to C and then C to P. VP−VR=(VP−VC)+(VC−VR)V_P - V_R = (V_P - V_C) + (V_C - V_R). We already found VP−VC=12BωR2V_P - V_C = \frac{1}{2}B\omega R^2. Path from R to C: r⃗CR=Rj^\vec{r}_{CR} = R\hat{j}. dl⃗=dyj^d\vec{l} = dy\hat{j} from y=Ry=R to y=0y=0. VC−VR=∫RC(v⃗×B⃗)⋅dl⃗=∫R0(−Bωxi^−Bω(R+y)j^)⋅(dyj^)V_C - V_R = \int_R^C (\vec{v} \times \vec{B}) \cdot d\vec{l} = \int_R^0 (-B\omega x\hat{i} - B\omega(R + y)\hat{j}) \cdot (dy\hat{j}). Along the path from R to C, x=0x=0. VC−VR=∫R0(−Bω(R+y)j^)⋅(dyj^)=∫R0−Bω(R+y)dyV_C - V_R = \int_R^0 (-B\omega(R + y)\hat{j}) \cdot (dy\hat{j}) = \int_R^0 -B\omega(R + y) dy VC−VR=−Bω[Ry+y22]R0=−Bω[0−(R(R)+R22)]=−Bω(−3R22)=32BωR2V_C - V_R = -B\omega \left[ Ry + \frac{y^2}{2} \right]_R^0 = -B\omega \left[ 0 - \left( R(R) + \frac{R^2}{2} \right) \right] = -B\omega \left( -\frac{3R^2}{2} \right) = \frac{3}{2}B\omega R^2. Therefore, VP−VR=(VP−VC)+(VC−VR)=12BωR2+32BωR2=2BωR2V_P - V_R = (V_P - V_C) + (V_C - V_R) = \frac{1}{2}B\omega R^2 + \frac{3}{2}B\omega R^2 = 2B\omega R^2. Since V=ωRV = \omega R, VP−VR=2BVRV_P - V_R = 2BVR.

  • VP−VSV_P - V_S: We integrate from S to P. Path from S to C and then C to P. VP−VS=(VP−VC)+(VC−VS)V_P - V_S = (V_P - V_C) + (V_C - V_S). We already found VP−VC=12BωR2V_P - V_C = \frac{1}{2}B\omega R^2. Path from S to C: r⃗CS=Ri^\vec{r}_{CS} = R\hat{i}. dl⃗=dxi^d\vec{l} = dx\hat{i} from x=Rx=R to x=0x=0. VC−VS=∫SC(v⃗×B⃗)⋅dl⃗=∫R0(−Bωxi^−Bω(R+y)j^)⋅(dxi^)V_C - V_S = \int_S^C (\vec{v} \times \vec{B}) \cdot d\vec{l} = \int_R^0 (-B\omega x\hat{i} - B\omega(R + y)\hat{j}) \cdot (dx\hat{i}). Along the path from S to C, y=0y=0. VC−VS=∫R0(−Bωxi^)⋅(dxi^)=∫R0−BωxdxV_C - V_S = \int_R^0 (-B\omega x\hat{i}) \cdot (dx\hat{i}) = \int_R^0 -B\omega x dx VC−VS=−Bω[x22]R0=−Bω[0−R22]=−Bω(−R22)=12BωR2V_C - V_S = -B\omega \left[ \frac{x^2}{2} \right]_R^0 = -B\omega \left[ 0 - \frac{R^2}{2} \right] = -B\omega \left( -\frac{R^2}{2} \right) = \frac{1}{2}B\omega R^2. Therefore, VP−VS=(VP−VC)+(VC−VS)=12BωR2+12BωR2=BωR2V_P - V_S = (V_P - V_C) + (V_C - V_S) = \frac{1}{2}B\omega R^2 + \frac{1}{2}B\omega R^2 = B\omega R^2. Since V=ωRV = \omega R, VP−VS=BVRV_P - V_S = BVR.

Summary of results: VP−VQ=BVRV_P - V_Q = BVR VP−VR=2BVRV_P - V_R = 2BVR $V_P - V_S = BVR