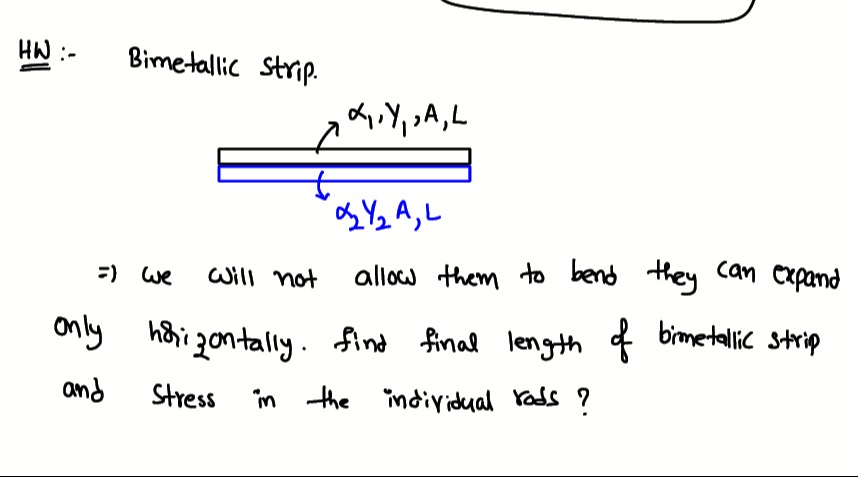
Question

We will not allow them to bend they can expand only horizontally. Find final length of bimetallic strip and Stress in the individual rods?

Answer 1

The final length of the bimetallic strip is: $L' = L \left[ 1 + \Delta T \left( \frac{\alpha_1 Y_1 + \alpha_2 Y_2}{Y_1 + Y_2} \right) \right]$ Stress in the first rod ($\sigma_1$): $\sigma_1 = \frac{Y_1 Y_2 (\alpha_2 - \alpha_1) \Delta T}{Y_1 + Y_2}$ Stress in the second rod ($\sigma_2$): $\sigma_2 = \frac{Y_1 Y_2 (\alpha_1 - \alpha_2) \Delta T}{Y_1 + Y_2}$

Answer 2

The bimetallic strip is constrained from bending, meaning both constituent rods must expand to the same final length. Let the temperature change be $\Delta T$. The difference in expansion is accommodated by internal stresses. Force balance requires that the stresses in the two rods are equal in magnitude and opposite in sign ($\sigma_1 = -\sigma_2$). By equating the total change in length for both rods, which is the sum of thermal expansion and elastic strain ($\Delta L = \alpha L \Delta T + \sigma L/Y$), and using the force balance condition, we can solve for the stresses and the final length of the strip. The final length can be expressed using an effective coefficient of thermal expansion, $\alpha_{eff} = \frac{\alpha_1 Y_1 + \alpha_2 Y_2}{Y_1 + Y_2}$.