Question

In the given figure, $AB=2,BC=6,AE=6,BF=8,CE=7\text{ and }CF=7.$ The ratio of ar ABDE to the $ar\Delta CDF$ is:
A. 1:1
B. 2:1
C. 1:2
D. None

Answer 1

To find the ratio of ar ABDE: ar $\Delta CDF$ we need to find the area of a quadrilateral ABDE & area of $\Delta CDF$. For that first we will observe the given figure, by this we will find that $\Delta ACE\And \Delta BCF$ is congruent. Then by taking Area of Quadrilateral $\text{ABDE = Area of }\Delta ACE\text{ }-\text{ Area of }\Delta BCD$ and $\text{Area of }\Delta CDF=\text{Area of }\Delta BCF-\text{ Area of }\Delta BCD$ . Then we can find the ratio by substituting the values.
Complete step-by-step answer:

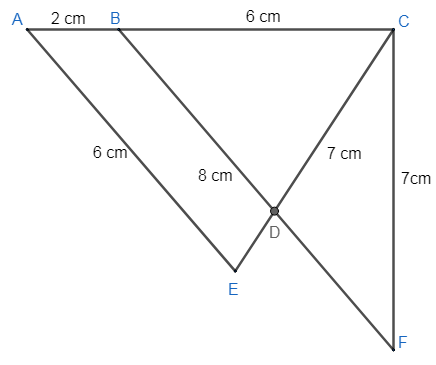
By observing the figure, we get to know that $AB=2,BC=6,AE=6,BF=8,CE=7,CF=7\text{ and }AC=AB+BC$.
By substituting the values of AB and BC, we get –
∃ΑΧ=2+6=8∃
We can also observe from the $\Delta ACE\And \Delta BCF$that –
$\begin{aligned} & AC=BF=8cm \\\ & AE=BC=6cm \\\ & CE=CF=7cm \\\ \end{aligned}$
As the sides of both the triangles are same, we can say that $\Delta ACE\And \Delta BCF$ are congruent.
Therefore, $\text{Area of }\Delta ACE=\text{ Area of }\Delta BCF$.
Let us consider ‘x’ as the $\text{Area of }\Delta ACE=\text{Area of }\Delta BCF=x$ ……………………………… (1)
Now, we need to find the ratio of the area of quadrilateral ABDE to the area of $\Delta CDF$.
To find this let us draw the figure and shade the area which we need to find.

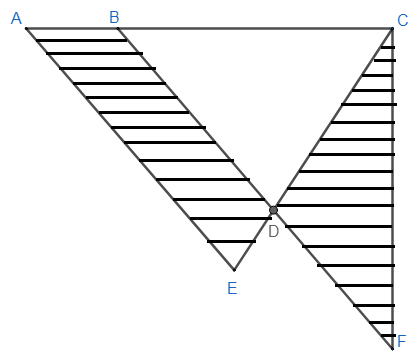
Here, the shaded regions are quadrilateral ABDE and $\Delta CDF$.
From the figure we get that –
Area of Quadrilateral $\text{ABDE = Area of }\Delta ACE\text{ }-\text{ Area of }\Delta BCD$
By substituting the value of $\Delta ACE$ from equation (1) we get –
Area of ABDE $=x-\Delta BCD$ …………………….. (2)
We can also observe that –
$\text{Area of }\Delta CDF=\text{Area of }\Delta BCF-\text{ Area of }\Delta BCD$.
By substituting the value of $\Delta ACE$ from equation (1) we get –
$\text{Area of }\Delta CDF=x-\Delta BCD$ ……………………….. (3)
Now, we will find the ration of ar ABDE: ar $\Delta CDF$
Therefore,
$\dfrac{\text{Area of Quadrilateral ABDE}}{\text{Area if }\Delta \text{CDF}}$
By substituting the values from equation (1) and (2) , we get that –
$\Rightarrow \dfrac{x-\Delta BCD}{x-\Delta BCD}$
By cancelling the common factors from numerator and denominator, we get –
$\Rightarrow \dfrac{1}{1}$
Therefore, the ration of ar ABDE: ar $\Delta CDF$ is 1:1
Hence, option A. is the correct answer.

Note: Students should know that, if all the sides of two triangles are proportional, then this is called SSS similarity and the two triangles called congruent or similar triangles.
For example: In our question –
For $\Delta ACE\And \Delta BCF$
$\dfrac{AE}{BC}=\dfrac{CE}{CF}=\dfrac{AC}{BF}$
By substituting their values, we get –
$\dfrac{6}{6}=\dfrac{7}{7}=\dfrac{8}{8}$
By cancelling the common factors from numerator and denominator, we get –
$1=1=1$
Therefore, it proves that $\Delta ACE\cong \Delta BCF$ which is congruent.