Question

How would you graph the line $x=3$? $$$$

Answer 1

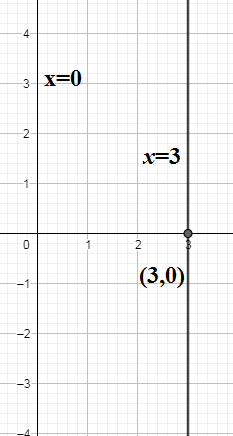
We recall the definition of $x$ and $y-$ coordinate of the point. We use the fact that that the locus of all points equidistant from a line will be a line parallel to the original line and deduce that $x=3$ is a line parallel to $y-$ axis at a distance 3 from $y-$ axis passing through point $\left( 3,0 \right)$.$$$$

Complete step by step answer:
We know that all points in plane are represented as the ordered pair $\left( a,b \right)$ where $\left| a \right|$ is the distance from $y-$axis (called as abscissa or $x-$coordinate) and $\left| b \right|$ is the distance of the point from the $y-$axis (called as ordinate or $y-$coordinate).
We are given the line $x=3$ in the question. Here $x=3$ means all the points on the line $x=3$the $x-$coordinate of the points will remain same irrespective of the $y-$ordinate which means $x=3$ is the locus points of the type $\left( 3,b \right)$ where $b\in R$. $$$$
We know that locus of all points equidistant from a line will be a line parallel to the original line. Since $x-$coordinate which is also the distance $\left( \left| 3 \right|=3 \right)$ from $y-$axis is constant, all the points from $y-$axis will be equidistant. So the distance between $y-$axis and $x=3$ is constant and hence $x=3$is line parallel to $y-$axis . So the line $x=3$ will also pass through $\left( 3,0 \right)$ where it will cut $x-$axis for the value $y=0$ in $\left( 3,b \right)$.

Note:
We know that the general equation of line is $ax+by+c=0$ and the line parallel to it is given by $ax=by+k=0,k\ne c$. Since the equation of the $y-$axis is $x=0$ line parallel to it will be $x=k,k\ne 0$. We can alternatively find the slope of the line $ax+by+c=0$ as $\dfrac{-a}{b}$ from $0\cdot y+1\cdot x-3=0$ as $\dfrac{-1}{0}=\infty$ that is undefined and we know that a lien with undefined slope is perpendicular to $x-$axis and we get point $\left( 3,0 \right)$ to draw the perpendicular line.