Solveeit Logo
Login

Question

Question: How would you graph the line \(2x + 8 = 0\)?...

How would you graph the line 2x+8=02x + 8 = 0?

Explanation

Solution

First step is to isolate the variable terms on one side by performing the same mathematical operations on both sides of the equation. Next step is to isolate the constant terms on the other side by performing the same mathematical operations on both sides of the equation. Next step is to make the coefficient of the variable equal to 11 using multiplication or division property. Next, draw graph AB of a line parallel to Y-axis at a distance of 4 units from Y-axis in the negative direction of X-axis.

Complete step by step answer:
The algebraic equation is 2x+8=02x + 8 = 0.
We have to find the value of xx.
First step is to isolate the variable terms on one side by performing the same mathematical operations on both sides of the equation.
Here, the variable term xx is already on one side of the equation.
Thus, 2x+8=02x + 8 = 0.
Next step is to isolate the constant terms on the other side by performing the same mathematical operations on both sides of the equation.
So, subtracting 88 from both sides of the equation 2x+8=02x + 8 = 0.
⇒2x+8−8=0−8\Rightarrow 2x + 8 - 8 = 0 - 8
It can be written as
⇒2x=−8\Rightarrow 2x = - 8
Next step is to make the coefficient of the variable equal to 11 using multiplication or division property.
So, divide both sides of the equation by 22, we get
⇒2x2=−82\Rightarrow \dfrac{{2x}}{2} = \dfrac{{ - 8}}{2}
Cancel the common factor.
∴x=−4\therefore x = - 4
If it is treated as an equation in two variables, then it can be written as 1⋅x+0⋅y+4=01 \cdot x + 0 \cdot y + 4 = 0 and it is represented by a line.
Here, all the values of yy are permissible, because 0⋅y0 \cdot y is always 00. However, xx must satisfy the equation 2x+8=02x + 8 = 0.

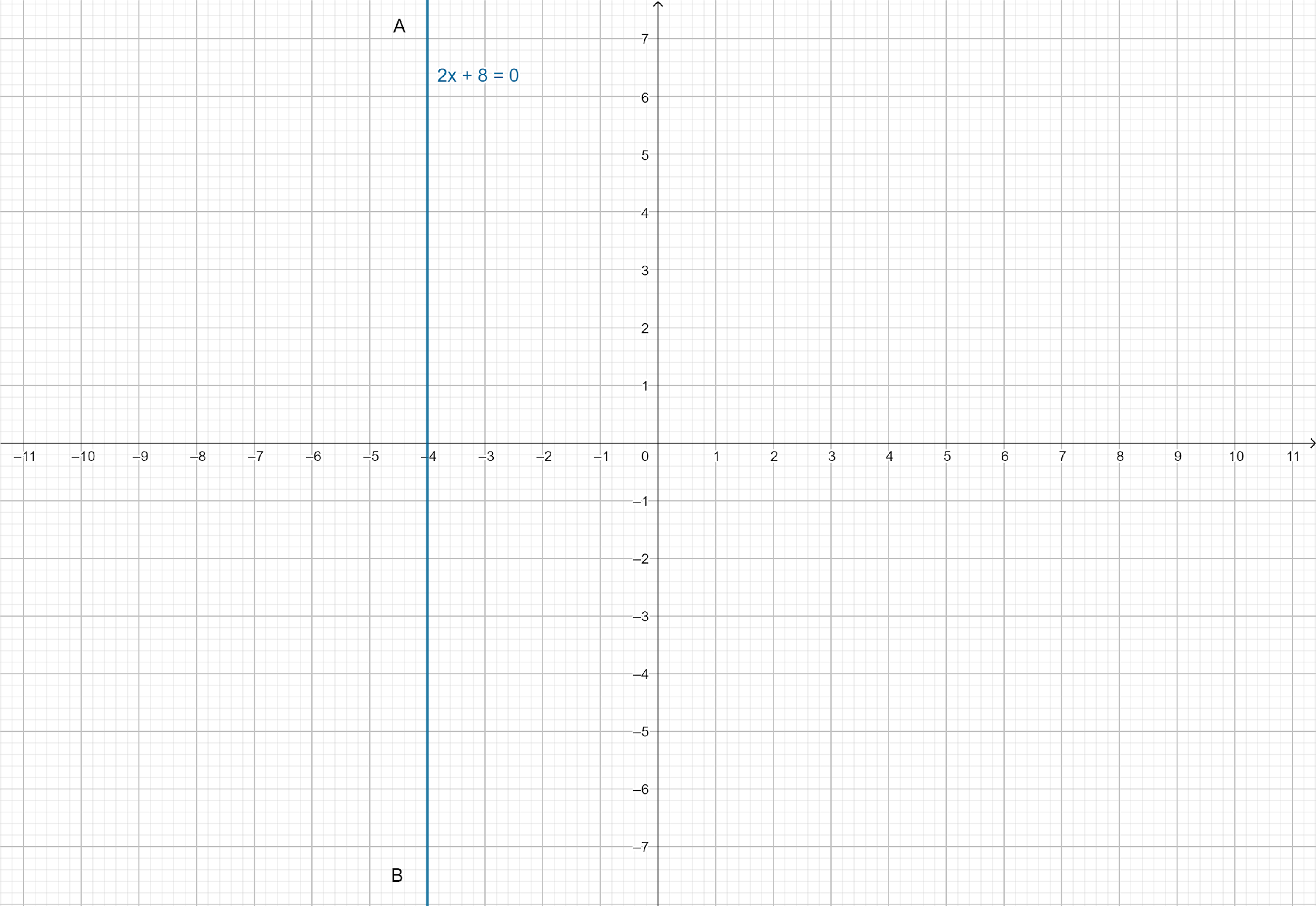
The graph AB is a line parallel to Y-axis at a distance of 4 units from Y-axis in the negative direction of X-axis.

Hence, the straight line, so obtained is the required graph of given linear equation.

Note: If a>0a > 0, then x=ax = a represent the equation of a line parallel to Y-axis in the positive direction of X-axis and x=−ax = - a in the negative direction of X-axis.