Question

How would you find the volume of the tetrahedron T bounded by the coordinate planes and the plane $3x + 4y + z = 10$ ?

Answer 1

Hint : Here we will follow a step by step approach, first we will find the coordinates for the tetrahedron and then we will frame the equation for the volume and will take double integration along with the limits on it and will simplify to get the resultant value.

Complete step-by-step answer :
The coordinate planes can be given by $x = 0,y = 0$ and $z = 0.$
The volume is that of a tetrahedron whose vertices are the intersections of the three of the four planes in the data.
In the given data the intersection of $x = 0,y = 0$ in the equation $3x + 4y + z = 10$ is
$(0,0,10)$ .
Similarly, the other three vertices are $\left( {\dfrac{{10}}{3},0,0} \right),\left( {0,\dfrac{5}{2},0} \right)$ and the origin $(0,0,0)$
The given tetrahedron T is the solid which lies above the triangle R in the xy-plane which has the vertices such as $(0,0),\left( {\dfrac{{10}}{3},0} \right)$ and $\left( {0,\dfrac{5}{2}} \right)$
Draw the diagram using the above vertices.

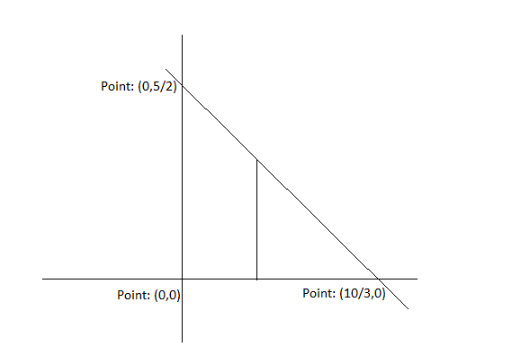
The line joining $\left( {0,\dfrac{5}{2}} \right)$ and $\left( {\dfrac{{10}}{3},0} \right)$ can be given by:
$y - 0 = \left( {\dfrac{{\dfrac{5}{2}}}{{\dfrac{{ - 10}}{3}}}} \right)\left( {x - \dfrac{{10}}{3}} \right)$
Simplify the above equation, denominator’s denominator goes to the numerator and the numerator’s denominator goes to the denominator.
$\Rightarrow y = \left( {\dfrac{5}{{ - 10}} \times \dfrac{3}{2}} \right)\left( {x - \dfrac{{10}}{3}} \right)$
Simplify the above equation:
$\Rightarrow y = \left( {\dfrac{{15}}{{ - 20}}x - \left( {\dfrac{{15}}{{ - 20}}} \right)\left( {\dfrac{{10}}{3}} \right)} \right)$
Common factors from the numerator and the denominator cancel each other. Also product of minus minus plus.
$\Rightarrow y = \left( {\dfrac{3}{{ - 4}}x + \left( {\dfrac{5}{2}} \right)} \right)$
Also, the region R can be defined as:
$R = \\{ (x,y)/0 \leqslant x \leqslant \dfrac{{10}}{3},0 \leqslant y \leqslant \dfrac{{ - 3}}{4}x + \dfrac{5}{2}\\}$
Now, the volume “V “ of the tetrahedron is the double integration of the function $z = 10 - 3x - 4y$ over the region R.
$\therefore V = \iint\limits_R {(10 - 3x - 4y)dA}$
Now place the limits in the above double integration-
$\therefore V = \int\limits_0^{10/3} {\int\limits_0^{\dfrac{{ - 3}}{4}x + \dfrac{5}{2}} {(10 - 3x - 4y)dydx} }$
Now apply first integration with respect to “dy” and then apply the limit to it.
$\therefore V = \int\limits_0^{10/3} {[(10 - 3x)\left( y \right) - 2{{\left( y \right)}^2}]_{y = 0}^{y = \dfrac{{ - 3}}{4}x + \dfrac{5}{2}}dx}$
Place the limits in the above expression.
\therefore V = \int\limits_0^{10/3} {[(10 - 3x)\left( {\dfrac{{ - 3x}}{4} + \dfrac{5}{2}} \right) - 2{{\left( {\dfrac{{ - 3x}}{4} + \dfrac{5}{2}} \right)}^2}\\} - \\{ 0\\} dx}
Simplify the above equation.
\therefore V = \int\limits_0^{10/3} {\left( {\dfrac{{ - 30x}}{4} + 25 + \dfrac{9}{4}{x^2} - \dfrac{{15}}{2}x} \right) - 2\left( {\dfrac{{9{x^2}}}{{16}} - \dfrac{{15}}{4}x + \dfrac{{25}}{4}} \right)\\} dx}
Simplify the above equation making the pair of like terms, and apply appropriate addition and subtraction in it.
$\therefore V = \int\limits_0^{10/3} {\left( {\dfrac{{ - 15x}}{2} + \dfrac{{25}}{2} + \dfrac{{9{x^2}}}{8}} \right)dx}$
Now, apply a second integration in the above expression.
$\therefore V = \left[ {\dfrac{{ - 15{x^2}}}{2} + \dfrac{{25}}{2}x + \dfrac{{9{x^3}}}{{24}}} \right]_0^{\dfrac{{10}}{3}}$
Apply limits in the above equation.
$\therefore V = \left[ {\dfrac{{ - 15}}{2}.\dfrac{{100}}{9} + \dfrac{{25}}{2}.\dfrac{{10}}{3} + \dfrac{9}{{24}}.\dfrac{{1000}}{{27}}} \right] - 0$
Common factors from the numerator and the denominator cancel each other.
$\therefore V = \left[ {\dfrac{{ - 125}}{3} + \dfrac{{125}}{3} + \dfrac{{125}}{9}} \right]$
Like terms with the same value and opposite sign cancel each other.
$\therefore V = \dfrac{{125}}{9}$ cubic units
So, the correct answer is “V = $\dfrac{{125}}{9}$ cubic units”.

Note : Always remember to put the relevant unit once you find the volume. Remember volume is measured in cubic units whereas, the area is measured in square units. Also, remember the standard formulas for the integration for the efficient and accurate solution.