Question

How would you find the center and radius of ${x^2} + {y^2} - 6x = 0$?

Answer 1

In this question, we have been given an equation of a circle.
The general equation of a circle is,
${(x - a)^2} + {(y - b)^2} = {r^2}$
Where, $(a,b)$ is a center, $r$ is a radius.
First, we group the same variables,
For example, ${x^2} + {y^2} - 4x - 16y = 0$ , we group the variables
${x^2} - 4x + {y^2} - 16y = 0$
And then we find the center and radius by using the square method.

Complete step by step answer:
The standard form for the equation of a circle with center $(a,b)$ and radius $r$ is,
${(x - a)^2} + {(y - b)^2} = {r^2}$
We need to convert the given equation into the standard equation.
${x^2} + {y^2} - 6x = 0$
Grouping the terms containing $x$, hence we get
${x^2} - 6x + {y^2} = 0$
Using completing the square method, we will add and subtract on both the sides by square of the half of the coefficient of $x$ , i.e., ${\left( {\dfrac{6}{2}} \right)^2} = {3^2} = 9$ , hence we get,
$({x^2} - 6x + {3^2}) - {3^2} + {y^2} = 0$
Shifting the constant to the other side,
$({x^2} - 6x + {3^2}) + {y^2} = {3^2}$
The ${(y - b)^2}$ term in the standard form can be written as ${(y - 0)^2}$.
Now the standard form of a circle is, we get
${(x - 3)^2} + {(y - 0)^2} = {3^2}$ ,
which is the required form of a circle with center at $(a,b)$ , hence we get,
Comparing the equation with the standard form of equation, we get,
$a = 3,b = 0$ and $r = 3$
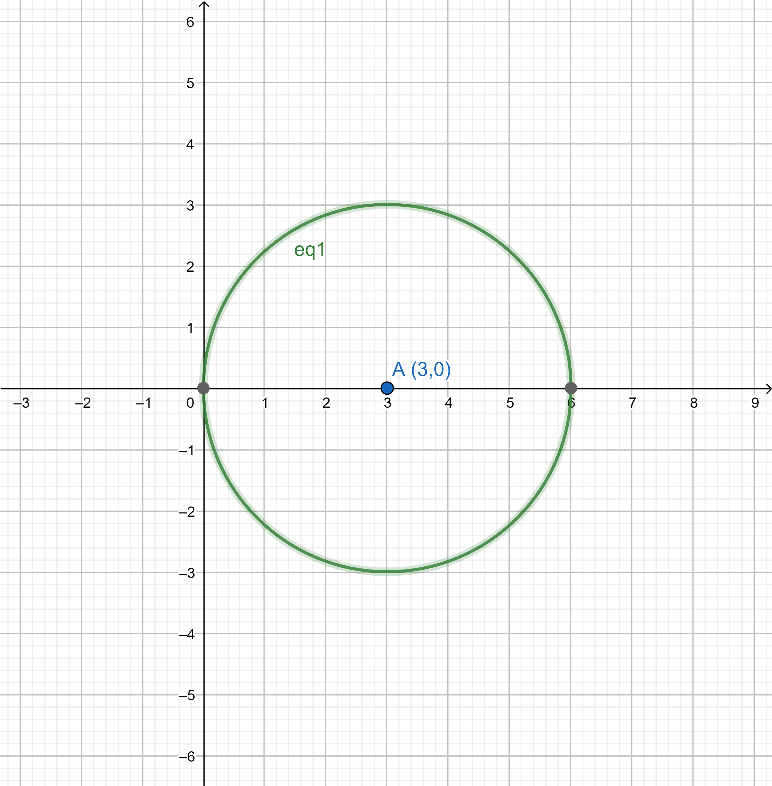
Then the center point is $(3,0)$
And the radius is $3$ .
Hence, this is how you find the center and the radius. Let us plot the equation on the graph.

Note: The general equation of a circle is
${x^2} + {y^2} + 2gx + 2fy + c = 0$
Where the center is given by $( - g, - f)$ and the radius is given by $r = \sqrt {{g^2} + {f^2} - c}$ . The equation can be recognized because it is given by a quadratic expression in both $x$ and $y$ with no $xy$ them, and where the coefficients of ${x^2}$ and ${y^2}$ are equal. We recognize it is quadratic in both $x$ and $y$, and it has two additional properties. First, there is no term in $xy$. And secondly, the coefficient of ${x^2}$ is the same as the coefficients of ${y^2}$. The centre of the circle is then at $(a,b) = ( - g, - f)$ and, since $c = {g^2} + {f^2} - {r^2}$ , we have
${r^2} = {g^2} + {f^2} - c$
So that the radius of the circle is given by,
$r = \sqrt {{g^2} + {f^2} - c}$