Question

How would I solve $\cos x + \cos 2x = 0$? Please show steps.

Answer 1

First, substitute $u$ for all occurrences of $\cos x$ and factor by grouping. Next, replace all occurrences of $u$ with $\cos x$. Next, set the factor on the left side of the equation equal to $0$ and solve for $x$ using trigonometric properties. Then, we will get all solutions of the given equation.

Formula used:
$\cos \left( {\pi - x} \right) = - \cos x$
$\cos 0 = 1$

Complete step by step solution:
Given equation: $\cos x + \cos 2x = 0$
We have to find all possible values of $x$ satisfying a given equation.
Let $u = \cos x$. Substitute $u$ for all occurrences of $\cos x$.
$u + 2{u^2} - 1 = 0$
Factor by grouping.
Reorder terms.
$2{u^2} + u - 1 = 0$
We know, for a polynomial of the form $a{x^2} + bx + c$, rewrite the middle term as a sum of two terms whose product $a \times c = 2 \times \left( { - 1} \right) = - 2$ and whose sum is $b = 1$.
Multiply by $1$.
$2{u^2} + 1u - 1 = 0$
Rewrite $1$ as $- 1$ plus $2$.
$2{u^2} + \left( { - 1 + 2} \right)u - 1 = 0$
Apply the distributive property.
$2{u^2} - u + 2u - 1 = 0$
Factor out the greatest common factor from each group.
Group the first two terms and the last two terms.
$\left( {2{u^2} - u} \right) + \left( {2u - 1} \right) = 0$
Factor out the greatest common factor (GCF) from each group.
$u\left( {2u - 1} \right) + 1\left( {2u - 1} \right) = 0$
Factor the polynomial by factoring out the greatest common factor, $2u - 1$.
$\left( {2u - 1} \right)\left( {u + 1} \right) = 0$
Now, replace all occurrences of $u$ with $\cos x$.
$\left( {2\cos x - 1} \right)\left( {\cos x + 1} \right) = 0$
If any individual factor on the left side of the equation is equal to $0$, the entire expression will be equal to $0$.
$2\cos x - 1 = 0$
$\cos x + 1 = 0$
Set the first factor equal to $0$ and solve.
Set the first factor equal to $0$.
$2\cos x - 1 = 0$
Add $1$ to both sides of the equation.
$2\cos x = 1$
Divide each term by $2$ and simplify.
$\cos x = \dfrac{1}{2}$
Take the inverse cosine of both sides of the equation to extract $x$ from inside the cosine.
$x = \arccos \left( {\dfrac{1}{2}} \right)$
The exact value of $\arccos \left( {\dfrac{1}{2}} \right)$ is $\dfrac{\pi }{3}$.
$x = \dfrac{\pi }{3}$
The cosine function is positive in the first and fourth quadrants. To find the second solution, subtract the reference angle from $2\pi$ to find the solution in the fourth quadrant.
$x = 2\pi - \dfrac{\pi }{3}$
$\Rightarrow x = \dfrac{{5\pi }}{3}$
Since, the period of the $\cos x$ function is $2\pi$ so values will repeat every $2\pi$ radians in both directions.
$x = \dfrac{\pi }{3} + 2n\pi ,\dfrac{{5\pi }}{3} + 2n\pi$, for any integer $n$
Now, set the next factor equal to $0$ and solve.
$\cos x + 1 = 0$
Subtract $1$ from both sides of the equation.
$\cos x = - 1$…(i)
Now, using the property $\cos \left( {\pi - x} \right) = - \cos x$ and $\cos 0 = 1$ in equation (i).
$\Rightarrow \cos x = - \cos 0$
$\Rightarrow \cos x = \cos \left( {\pi - 0} \right)$
$\Rightarrow x = \pi$
Since, the period of the $\cos x$ function is $2\pi$ so values will repeat every $2\pi$ radians in both directions.
$x = \pi + 2n\pi$, for any integer $n$.
Final solution: Hence, $x = \dfrac{\pi }{3} + 2n\pi ,\dfrac{{5\pi }}{3} + 2n\pi ,\pi + 2n\pi$ or $x = \dfrac{\pi }{3} + \dfrac{{2n\pi }}{3}$, for any integer $n$are solutions of the given equation.

Note:
In the above question, we can find the solutions of a given equation by plotting the equation, $\cos x + \cos 2x = 0$ on graph paper and determine all its solutions.

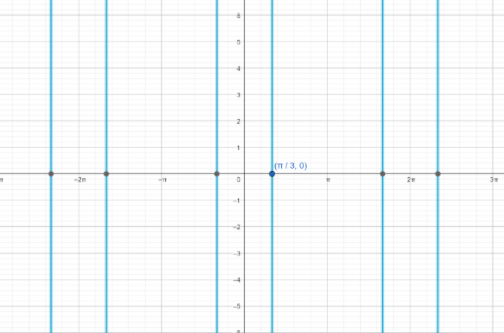
From the graph paper, we can see that $x = \dfrac{\pi }{3}$ is a solution of given equation, and solution repeat every $\dfrac{{2\pi }}{3}$ radians in both directions.
So, these will be the solutions of the given equation.
Final solution: Hence, $x = \dfrac{\pi }{3} + \dfrac{{2n\pi }}{3}$, for any integer $n$are solutions of the given equation.