Question

How will you prove the trigonometric formula Cos(A+B) = Cos A Cos B – Sin A Sin B using the formula of the cross product of two vectors1?

Answer 1

The cross product of two vectors is also a vector quantity The cross product a$\times$b is defined as a vector c that is perpendicular to both a and b, with a direction given by the right-hand rule and a magnitude equal to the area of the parallelogram that the vectors span.
$A \times B = \left | A \right |\left | B \right |\operatorname{Sin} \theta n$
Where
$\left | A \right |$ is the length of vector A
$\left | B \right |$ is the length of vector B
Is the angle between A & B
N is the unit vector perpendicular to the plane containing A and B

Complete step by step solution:
Refer to the following image

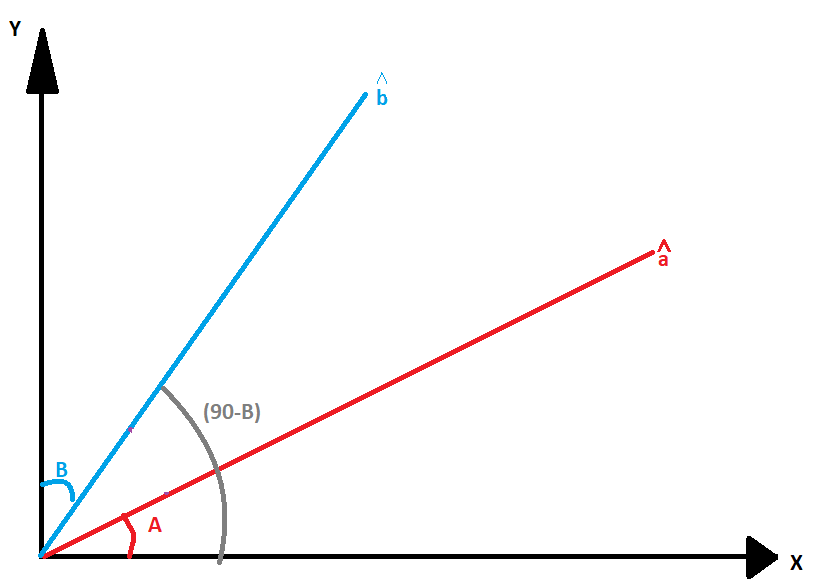
Now, consider two unit vectors in the X-Y plane as follows :
$\hat a$→ unit vector inclined with the positive direction of X-axis at angles A
$\hat b$→ unit vector inclined with the positive direction of X-axis at angles 90-B, where $90 - B > A$
The angle between these two vectors becomes
$\theta = 90 - A - B = 90 - \left( {A + B} \right)$
Now writing in vector form we get
$\hat a = \operatorname{Cos} A\hat i + \operatorname{Sin} A\hat j$
$\hat b = \operatorname{Cos} \left( {90 - B} \right)\hat i + \operatorname{Sin} \left( {90 - B} \right)\hat j$
$\hat b = \operatorname{Sin} B\hat i + \operatorname{Cos} B\hat j$
Now
Taking the cross product of the above two vectors i.e.,
$\hat a \times \hat b = \left( {\operatorname{Cos} A\hat i + \operatorname{Sin} A\hat j} \right) \times \left( {\operatorname{Sin} B\hat i + \operatorname{Cos} B\hat j} \right)$
$\because A \times B = \left | A \right |\left | B \right |\operatorname{Sin} \theta \hat k$
$\therefore \left | {\hat a} \right | \left | {\hat b} \right |\operatorname{Sin} \theta \hat k = \operatorname{Cos} A\operatorname{Cos} B\left( {\hat i \times \hat j} \right) + \operatorname{Sin} A\operatorname{Sin} B(\hat j \times \hat i)$ Applying Properties of unit vectors $\hat i,\hat j,\hat k$
$\hat i \times \hat j = \hat k$ $\hat j \times \hat i = - \hat k$
$\hat i \times \hat i = null$ $\hat j \times \hat j = null$ and
$\left | A \right |$=1 and $\left | B \right |$=1 as both are unit vectors
Also substituting the value of the angle between the vectors, $\theta = 90 - \left( {A + B} \right)$
Finally, we get,
$\operatorname{Sin} \left( {90 - \left( {A + B} \right)} \right)\hat k = \operatorname{Cos} A\operatorname{Cos} B\hat k + \operatorname{Sin} A\operatorname{Sin} B\hat k$
$\therefore \operatorname{Cos} \left( {A + B} \right) = \operatorname{Cos} A\operatorname{Cos} B - \operatorname{Sin} A\operatorname{Sin} B$

Note:
The Cross product is a vector quantity
If two vectors are parallel to each other then their cross product will be zero since $\operatorname{Sin} 0^\circ = 0$
The dot product is a scalar quantity
If two vectors are perpendicular their dot product will be zero since $\operatorname{Cos} 90^\circ = 0$