Question

How will you prove the formula$\cos \left( A-B \right)=\cos A\cos B+\sin A\sin B$ using the formula of the vector product of the two vectors?

Answer 1

First we have to draw two units vectors in xy plane both with the angle A and angle B with the total angle of (A+B) then after using the method of the dot product of the vectors we can prove formula which is given in the question.
Formula used:
$\overrightarrow{A}.\overrightarrow{B}=\left| \overrightarrow{A} \right|\left| \overrightarrow{B} \right|\cos \theta$

Complete answer:

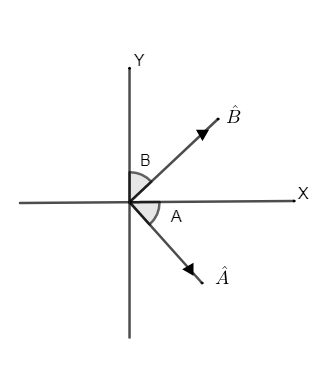
As shown in the figure, first draw the two vectors in x-y plane one makes an angle A with the x-axis and other one makes an angle B with the x-axis and the both have a total angle of (A+B).
Now in Cartesian form the vector $\widehat{A}\text{ and}\widehat{B}$ with their components can be written as,
$\widehat{A}=\cos A\widehat{i}-\sin A\widehat{j}...\left( 1 \right)$
And the vector$\widehat{B}$is,
$\widehat{B}=\cos B\widehat{i}+\sin B\widehat{j}...\left( 2 \right)$
Now let’s take the dot product of the two vectors,
$\overrightarrow{A}.\overrightarrow{B}=\left| \overrightarrow{A} \right|\left| \overrightarrow{B} \right|\cos \theta$
It should be consider that the resultant component will be in direction of $\widehat{k}$ hence,
$\overrightarrow{A}.\overrightarrow{B}=\left| \overrightarrow{A} \right|\left| \overrightarrow{B} \right|\sin \theta \widehat{k}...\left( 3 \right)$
Here the total angle θ = 90+B-A and the both vectors are unit vectors hence we can take,
$\left| \overrightarrow{A} \right|=\left| \overrightarrow{B} \right|=1...\left( 4 \right)$
Now substitute value of the equation (1) (2) and in equation (3)

& \left( \cos A\widehat{i}-\sin A\widehat{j} \right)\left( \cos B\widehat{i}-\sin B\widehat{j} \right)-\cos \left( 90+B-A \right) \\\ & \Rightarrow \sin \left( 90-\left( A-B \right) \right)\widehat{k}=\cos A\cos B\widehat{k}+\sin A\sin B\widehat{k} \\\ \end{aligned}$$ Taking $$\widehat{k}$$vector common and substituting, $\sin \left( 90-A-B \right)=\cos \left( A-B \right)$ We will get, $\therefore \cos \left( A-B \right)=\cos A\cos B+\sin A\sin B$ **Note:** While multiplying vectors $$\widehat{i},\widehat{j}\text{ and }\widehat{k}$$ please refer below rules to avoid mistakes, $$\begin{aligned} & \widehat{i}\times \widehat{j}=\widehat{k} \\\ & \widehat{j}\times \widehat{i}=-\widehat{k} \\\ & \widehat{i}\times \widehat{i}=\text{null vector} \\\ & \widehat{j}\times \widehat{j}=\text{null vector} \\\ \end{aligned}$$