Question

How will you graph the inequality $6x+5y<-30$?

Answer 1

Now to plot the graph we will first consider the corresponding equality. Now we will first write the equation such that we get y in terms of x. Now we will substitute the value of x and find the corresponding value of y. Hence we will get the point (x, y) on the line. Now we will use these points to plot the equation of line. Now take points on both sides of the line and check which part satisfies the inequality. Hence we will get the required graph.

Complete step by step solution:
Now to graph the inequality we will first make a graph of the line $6x+5y=-30$.
Now to draw the graph of the equation we will need to find at least two points (x, y) such that it satisfies the given equation. Then we will draw a line passing through the points.
Now let us rearrange the terms of the equation such that we can express y as a function of x.
$\Rightarrow 5y=-30-6x$
Now dividing the whole equation by 5 we get,
$\Rightarrow y=-6-\dfrac{6}{5}x$
Hence we have y in terms of x.
Now let us substitute x = 0. Then we get y = -6.
Hence (0, -6) is a point on the line.
Now let us substitute x = - 5 then we get $y=-6-6\left( \dfrac{-5}{5} \right)=0$
Hence we have (- 5, 0) is a point on the line.
Now let us plot the points (0, -6) and (-5, 0) on the graph and draw a line passing through the points.

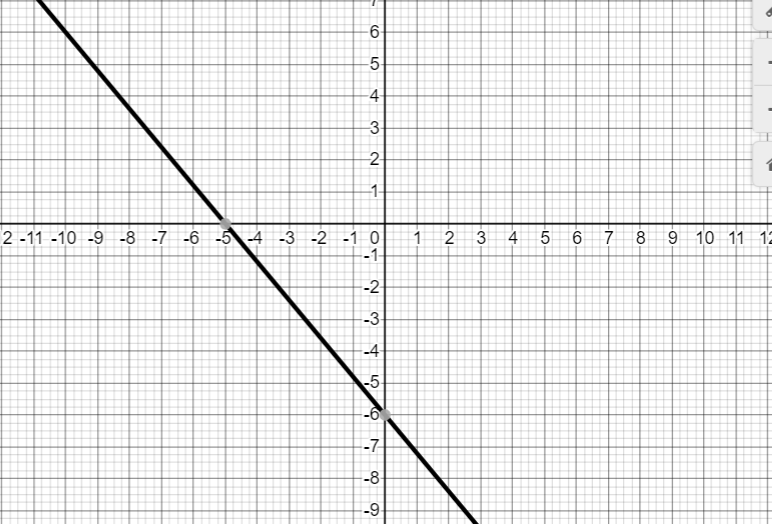
Now since we want inequality $6x+5y<-30$
Let us check any point below the line let us say (0, -7) then we have 6(0) + 5(-7) = -35 which is less than -30.
Now since the equation holds for one point below the line we can say that the equation holds for all point below the line. Hence the graph of inequality is.

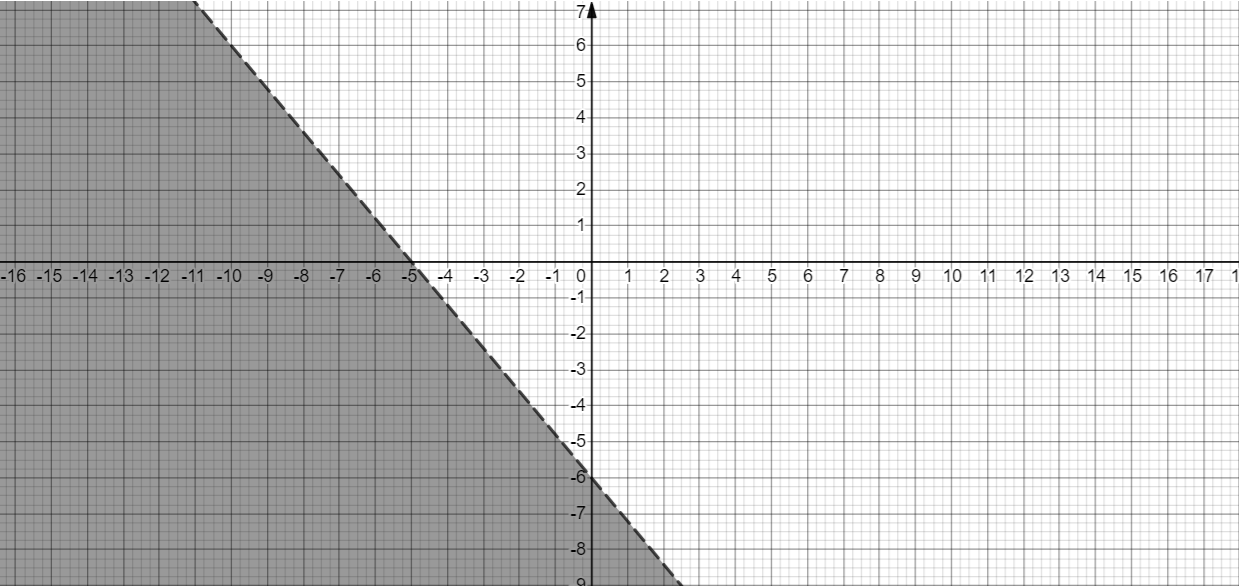
Note:
Now while drawing inequalities always note that first draw the line where equality holds. Now this line will divide the graph in two parts. One part where the inequality holds other where the inequality does not hold. Hence we will find the area by selecting any one point and checking if the equality holds.