Solveeit Logo
Login

Question

Question: How will you graph \[g(x) = {\left( {\dfrac{5}{8}} \right)^x}\]?...

How will you graph g(x)=(58)xg(x) = {\left( {\dfrac{5}{8}} \right)^x}?

Explanation

Solution

In order for solving the above problem we can substitute yy forg(x)g(x). Here we are asked to draw the graph of g(x)=(58)xg(x) = {\left( {\dfrac{5}{8}} \right)^x}and we are aware that exponential functions have horizontal asymptote which is basically a line on a graph that is approached by a curve but never reached. Remember that y=0y = 0 is the equation of horizontal asymptote.

Formula used:
Substituting yy for g(x)g(x), then determining the point and later on sketching the curve though the points by plotting it will give the graph

Complete step by step solution:
Firstly we will substitute yy for g(x)g(x) which means
y=(58)xy = {\left( {\dfrac{5}{8}} \right)^x}
Now we will determine the points which includes substituting the value of x including positive and negative numbers both and then solve for yy

x=−2, y = 2.56 x=−1, y = 1.6 x=0, y = 1 x=1, y = 0.625 x=2, y = 0.39 x=3, y = 0.24 x=7, y = 0.037  x = - 2,{\text{ y = 2}}{\text{.56}} \\\ x = - 1,{\text{ y = 1}}{\text{.6}} \\\ x = 0,{\text{ y = 1}} \\\ x = 1,{\text{ y = 0}}{\text{.625}} \\\ x = 2,{\text{ y = 0}}{\text{.39}} \\\ x = 3,{\text{ y = 0}}{\text{.24}} \\\ x = 7,{\text{ y = 0}}{\text{.037}} \\\

Later on we will plot the points and sketch a curve through the point
So graph for y=(58)x[−10,10,−5,5]\\{ y = {\left( {\dfrac{5}{8}} \right)^x}[ - 10,10, - 5,5]\\}
Using the above information we can plot a graph as followed

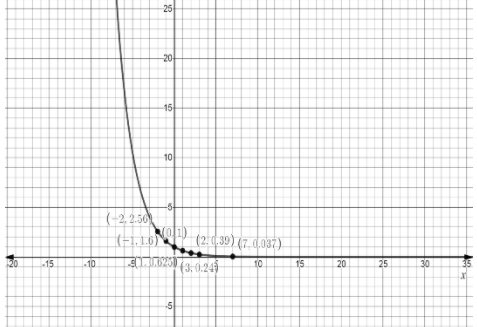
Additional Information:
Keep in mind that a horizontal asymptote is technically limited (x=∞x = \infty or x=−∞x = - \infty ) and due to this end behavior of function is measured by it. The graph of the function includes all the values of xx and the corresponding values of yy that are possible and due to this the graph is a line and not just the dots.

Note:
In the above problem we need to determine the points on the line then we need to plot the points and later on a sketch is curved throughout the point. Keep in mind of not connecting the dots. Exponential functions have horizontal asymptote and the equation of this horizontal asymptote is y=0y = 0. Keep in mind that while graphing a function the most significant and helpful step is to make a table of values and inclusion of negative value, positive value and zero for ensuring that we have a linear function is a good idea.