Question

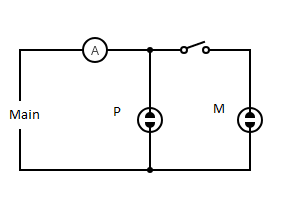
How will the reading in the ammeter $A$ be affected if another identical bulb $Q$ is connected in parallel to $P$ (Fig). The voltage in the mains is maintained at a constant value.

A) The reading will be reduced to one-half
B) The reading will not be affected
C) The reading will be double the previous value
D) The reading will be increased four-fold

Answer 1

The main supplies a potential difference which originates a current flow through the circuit. The bulbs on the other hand use the current flow through them to glow. The resistance in the bulb causes some voltage drop and eventually reduces the current flow. The ammeter in the circuit takes the reading of the current flow in the circuit.

Formula Used:
If a circuit has a source of potential $V$ and an effective resistance $R$ then the current flow through the circuit can be calculated as
$I = \dfrac{V}{R}$

Complete step by step answer:
Step 1:
You can see from the figure that the ammeter $A$ notes the reading of the current through the circuit.
You can ideally take the resistance of the ammeter to be $0$.
Hence, there will be no potential drop across the ammeter $A$ .
So, from eq (1), the reading of the ammeter can be defined as
$I = \dfrac{{{V_{main}}}}{{{R_{circuit}}}}$
where the main supplies a potential difference of ${V_{main}}$ and ${R_{circuit}}$ is the equivalent resistance of the circuit.
Step 2:
Let the main supplies a potential difference of ${V_{main}} = V$
When the switch is open, the circuit is connected to only the bulb $P$ .
Let the bulb have a resistance $R$ and hence the effective resistance in the circuit is ${R_{circuit}} = R$.
Hence, calculate the reading ${I_1}$ of the ammeter $A$ from the eq (2)
${I_1} = \dfrac{{{V_{main}}}}{{{R_{circuit}}}} \\\ \Rightarrow {I_1} = \dfrac{V}{R} \\\$
Therefore, the reading of the ammeter is ${I_1} = \dfrac{V}{R}$.
Step 3:
When the switch is closed, the circuit is connected to the bulb $P$ and the bulb $M$ parallelly.
By the problem, $P$ and $M$ are two identical bulbs.
Hence, the bulb has a resistance $R$ .
Calculate the effective resistance in the circuit.
$\dfrac{1}{{{R_{circuit}}}} = \dfrac{1}{R} + \dfrac{1}{R} \\\ \Rightarrow \dfrac{1}{{{R_{circuit}}}} = \dfrac{2}{R} \\\ \Rightarrow {R_{circuit}} = \dfrac{R}{2} \\\$
Hence, calculate the reading of the ammeter $A$ from the eq (2)
${I_2} = \dfrac{{{V_{main}}}}{{{R_{circuit}}}} \\\ \Rightarrow {I_2} = \dfrac{V}{{\dfrac{R}{2}}} \\\ \Rightarrow {I_2} = 2\dfrac{V}{R} \\\$
Therefore, the reading of the ammeter is ${I_2} = 2\dfrac{V}{R}$.
Step 4:
Hence, compare the two readings of the ammeter.
${I_2} = 2\dfrac{V}{R} = 2{I_1}$
$\therefore {I_2} = 2{I_1}$.

Final Answer:
If the ammeter $A$ is affected by connecting another identical bulb $Q$ in parallel to $P$ with the voltage in the mains, maintained at a constant value, then (C) The reading will be double the previous value.

Note: The identical bulbs should have the same resistance. You should neglect the internal resistance of the wires or the ammeter for the simplicity of the calculation. When the switch is open, the bulb $M$ shall not be connected to the circuit, but when the switch is closed, you should take the parallel connection as mentioned in the problem. The resistance of the bulbs can only cause a potential drop else, current flow through them remains unchanged.