Solveeit Logo
Login

Question

Question: How to write \(2{\tan ^{ - 1}}x\) in terms of \(\dfrac{{1 - {x^2}}}{{1 + {x^2}}}\) or \(\dfrac{{2x}}...

How to write 2tan⁡−1x2{\tan ^{ - 1}}x in terms of 1−x21+x2\dfrac{{1 - {x^2}}}{{1 + {x^2}}} or 2x1+x2\dfrac{{2x}}{{1 + {x^2}}}

Explanation

Solution

Hint – In this particular question first apply the tan rule (i.e. tan⁡−1C+tan⁡−1D=tan⁡−1(C+D1−CD){\tan ^{ - 1}}C + {\tan ^{ - 1}}D = {\tan ^{ - 1}}\left( {\dfrac{{C + D}}{{1 - CD}}} \right)) then use the basic trigonometric properties of sine, cosine and tan such as sine is the ratio of the perpendicular to the hypotenuse so use this concept to reach the solution of the question.

Complete step-by-step solution -

__
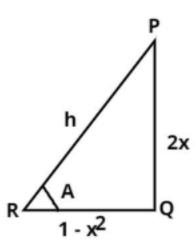
Let, A = 2tan⁡−1x2{\tan ^{ - 1}}x...................... (1)
Now as we know that tan⁡−1C+tan⁡−1D=tan⁡−1(C+D1−CD){\tan ^{ - 1}}C + {\tan ^{ - 1}}D = {\tan ^{ - 1}}\left( {\dfrac{{C + D}}{{1 - CD}}} \right)
So use this property in the above equation we have,
A = tan⁡−1x+tan⁡−1x{\tan ^{ - 1}}x + {\tan ^{ - 1}}x
⇒A=tan⁡−1(x+x1−x2)=tan⁡−1(2x1−x2)\Rightarrow A = {\tan ^{ - 1}}\left( {\dfrac{{x + x}}{{1 - {x^2}}}} \right) = {\tan ^{ - 1}}\left( {\dfrac{{2x}}{{1 - {x^2}}}} \right)
Now take tan inverse into R.H.S we have,
⇒tan⁡A=2x1−x2\Rightarrow \tan A = \dfrac{{2x}}{{1 - {x^2}}}
Now as we know tan is the ratio of the perpendicular to the base.
So in the above equation angle is (A) perpendicular is 2x and base is (1−x21 - {x^2}) as shown in the figure.
Consider the triangle PQR, in which PQ is the perpendicular, QR is the base and PR is the hypotenuse.
Let PR = h unit.
Now apply Pythagoras theorem in the triangle PQR we have,
⇒(hypotenuse)2=(perpendicular)2+(base)2\Rightarrow {\left( {{\text{hypotenuse}}} \right)^2} = {\left( {{\text{perpendicular}}} \right)^2} + {\left( {{\text{base}}} \right)^2}
⇒(h)2=(PQ)2+(QR)2\Rightarrow {\left( {\text{h}} \right)^2} = {\left( {{\text{PQ}}} \right)^2} + {\left( {{\text{QR}}} \right)^2}
⇒(h)2=(2x)2+(1−x2)2=4x2+1+x4−2x2=x4+2x2+1=(x2+1)2\Rightarrow {\left( h \right)^2} = {\left( {2x} \right)^2} + {\left( {1 - {x^2}} \right)^2} = 4{x^2} + 1 + {x^4} - 2{x^2} = {x^4} + 2{x^2} + 1 = {\left( {{x^2} + 1} \right)^2}
So the hypotenuse is h=x2+1h = {x^2} + 1
Now as we know that in any right triangle sine is the ratio of the perpendicular to hypotenuse
Therefore in triangle PQR, sin⁡A=2x1+x2\sin A = \dfrac{{2x}}{{1 + {x^2}}}
Therefore, A=sin⁡−1(2x1+x2)A = {\sin ^{ - 1}}\left( {\dfrac{{2x}}{{1 + {x^2}}}} \right).................. (2)
Now as we know that in any right triangle cosine is the ratio of the base to hypotenuse
Therefore in triangle PQR, cos⁡A=1−x21+x2\cos A = \dfrac{{1 - {x^2}}}{{1 + {x^2}}}
Therefore, A=cos⁡−1(1−x21+x2)A = {\cos ^{ - 1}}\left( {\dfrac{{1 - {x^2}}}{{1 + {x^2}}}} \right).................. (3)
Now from equation (1) and (2) we have,
⇒2tan⁡−1x=sin⁡−1(2x1+x2)\Rightarrow 2{\tan ^{ - 1}}x = {\sin ^{ - 1}}\left( {\dfrac{{2x}}{{1 + {x^2}}}} \right)
And from equation (1) and (3) we have,
⇒2tan⁡−1x=cos⁡−1(1−x21+x2)\Rightarrow 2{\tan ^{ - 1}}x = {\cos ^{ - 1}}\left( {\dfrac{{1 - {x^2}}}{{1 + {x^2}}}} \right)
So this is the required expression of 2tan⁡−1x2{\tan ^{ - 1}}x in terms of 1−x21+x2\dfrac{{1 - {x^2}}}{{1 + {x^2}}} or 2x1+x2\dfrac{{2x}}{{1 + {x^2}}}
So this is the required answer.

Note – Whenever we face such types of questions the key concept we have to remember is that in any right angle triangle the sine is the ratio of the perpendicular to the hypotenuse, the cosine is the ratio of base to hypotenuse and tan is the ratio of perpendicular to the base so first calculate the hypotenuse value by using the Pythagoras theorem as above then using the above stated properties calculate the values of sine and cosine of the angle A and equate them, we will get the required relation.