Question

How to solve the equation ${{\left( \ln x \right)}^{2}}=2x$

Answer 1

For these kinds of questions, all we need to do is solve for the values of $x$. Solving for the values of $x$ is nothing but finding out the point of intersection of these two curves. For functions which are quite simple , we can just solve for the value of $x$. But for the kind of functions given in the Question, it is better to go graphically. So we draw both the graphs of the curves and find out all the points of their intersection and this is how we solve them.

Complete step-by-step solution:
We don’t know the graph of ${{\left( \ln x \right)}^{2}}=2x$. So what we do here is equate each curve to variable $y$.
Since these two are equal to other variables, these two would in turn are equal to each other. This is a mild manipulation that we do.
Before equating each of them to $y$, we should acknowledge the fact that the graph of ${{\left( \ln x \right)}^{2}}$ is not something we remember on a daily basis. It should be traced using rules of differentiation. But the curve $\left( \ln x \right)$ is a common one that we all study before starting algebra.
So that is why we should apply square roots on both sides so that we get out the common $\left( \ln x \right)$ that we can graph.
Upon taking square root on both sides, we get the following :
$\begin{aligned} & \Rightarrow {{\left( \ln x \right)}^{2}}=2x \\\ & \Rightarrow \left( \ln x \right)=\pm \sqrt{2x} \\\ \end{aligned}$
$\pm \sqrt{2x}$ is nothing but a simple parabola curve which has its vertex as the origin and principal axis as the positive $x$- axis.
Let us now equate each to $y$. Upon doing so, we get the following :
$\begin{aligned} & \Rightarrow y=\left( \ln x \right) \\\ & \Rightarrow y=\pm \sqrt{2x} \\\ \end{aligned}$
Let us graph them now.
Upon graphing, we get the following :

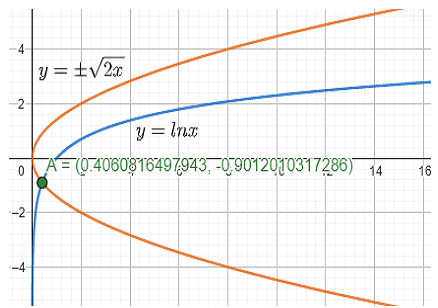
We can see that they only intersected at one point i.e A.

Note: In the exam, we would definitely not be asked about the values of $x$ since finding out it’s value is not a competitive exam friendly question. We would be asked about the number of points of intersection of both these graphs. We should be able to graph some basic curves such as ${{e}^{x}},\left( \ln x \right),\dfrac{2}{1+{{x}^{2}}}$ , all the trigonometric functions and their inverses, parabolas. We can’t sit in the exam and trace them .