Question

How to solve $3{\tan ^3}x = \tan x$ in the interval where $x$ belongs to 0 to $2 \pi$?

Answer 1

In this type of trigonometric questions we bring all the terms in RHS to LHS and then we try to take out as many terms as are common. Since RHS is zero, after solving we can easily get all the possible values of x that satisfy.

Complete step-by-step solution:
So initially we will take all the terms from RHS to LHS, which will be giving us with,
\Rightarrow $$$$3{\tan ^3}x - \tan x = 0
Now we will take all common terms out, which will be giving us with,
\Rightarrow $$$$\tan x\left( {3{{\tan }^2}x - 1} \right) = 0
Now when we equate the above equation to zero, either
\Rightarrow $$$$\tan x=$0$ or $\left( {3{{\tan }^2}x - 1} \right) = 0$
\Rightarrow $$$$\tan x=$0$ OR $\tan x$=$\pm \dfrac{1}{{\sqrt 3 }}$

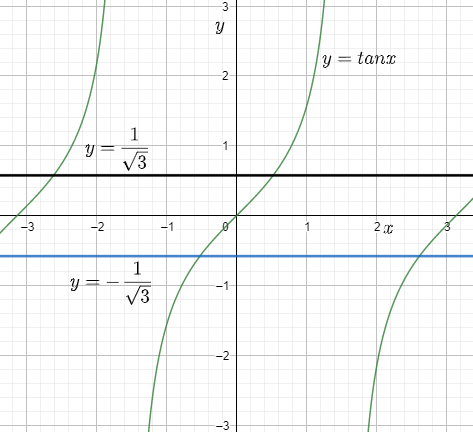
Above given is the graph of tan x and the red line is y=$\dfrac{1}{{\sqrt 3 }}$ and the grey line below the axis is y=-$\dfrac{1}{{\sqrt 3 }}$.
Clearly in the graph we can see that there are 5 points of intersection out of which x=0, $\pi$ are two.
We know that, in the interval where $x$ belongs to 0 to $2\pi$
$\tan x$=$\dfrac{1}{{\sqrt 3 }}$ at $x$= $\dfrac{\pi }{6}$ , $\dfrac{{7\pi }}{6}$ and $\tan x$=-$\dfrac{1}{{\sqrt 3 }}$ at x= $\dfrac{{5\pi }}{6}$
Therefore the 5 solutions to the equation are:-
$x = 0$ , $\pi$,$\dfrac{\pi }{6}$ , $\dfrac{{7\pi }}{6}$, $\dfrac{{5\pi }}{6}$.

Note: In such types of trigonometric questions, while finding the final solutions we sometimes get confused between angles. That means we sometimes get confused $\dfrac{\pi }{6}$ and $\dfrac{\pi }{3}$. In other words, we sometimes write $\tan x$=$\dfrac{1}{{\sqrt 3 }}$ at $x$=$\dfrac{\pi }{3}$ and so on. This should be avoided and taken care of.