Solveeit Logo
Login

Question

Question: How to simplify \( \tan \left( {arcs\sin \left( x \right)} \right) \) ?...

How to simplify tan⁡(arcssin⁡(x))\tan \left( {arcs\sin \left( x \right)} \right) ?

Explanation

Solution

Hint : In this question, we need to simplify tan⁡(arcssin⁡(x))\tan \left( {arcs\sin \left( x \right)} \right) . First of all, you must be wondering what arc means. In trigonometry, arc means the inverse of a function. So, arcsin⁡(x)\arcsin \left( x \right) means sin⁡−1x{\sin ^{ - 1}}x . To solve this question, we are going to suppose sin⁡−1x=θ{\sin ^{ - 1}}x = \theta and then substitute it in our expression. Then, we find the value of sin⁡θ\sin \theta and then draw a right angled triangle in which two sides will be given by sin⁡θ\sin \theta and for finding the third side, we will use Pythagora's theorem. On finding all the three sides, we will get the answer to our question.

Complete step by step solution:
Given expression: tan⁡(arcssin⁡(x))\tan \left( {arcs\sin \left( x \right)} \right)
=tan⁡(sin⁡−1x)−−−−(1)= \tan \left( {{{\sin }^{ - 1}}x} \right) - - - - \left( 1 \right)
Let
sin⁡−1x=θ ⇒sin⁡θ=x−−−−(2)  {\sin ^{ - 1}}x = \theta \\\ \Rightarrow \sin \theta = x - - - - \left( 2 \right) \\\
Putting this value in equation (1), we get
tan⁡(arcssin⁡(x))=tan⁡θ\tan \left( {arcs\sin \left( x \right)} \right) = \tan \theta
Now to find our answer, we need to find the value of tan⁡θ\tan \theta .
For that, we are going to use equation (2) to draw a right angled triangle.
As we know that sin⁡θ=oppositehypotenuse\sin \theta = \dfrac{{opposite}}{{hypotenuse}}
AB=opposite=x AC=hypotenuse=1 BC=Base=a   AB = opposite = x \\\ AC = hypotenuse = 1 \\\ BC = Base = a \;

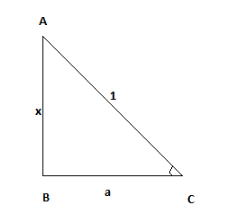
Now to find the value of tan⁡θ\tan \theta we need to find the value of a.
We are going to use the Pythagorean Theorem to find the value of a.
The Pythagoras theorem states that the square of hypotenuse is equal to the sum of squares of the other two sides.
AB2+BC2=AC2 x2+a2=12 a2=1−x2 a=1−x2   A{B^2} + B{C^2} = A{C^2} \\\ {x^2} + {a^2} = {1^2} \\\ {a^2} = 1 - {x^2} \\\ a = \sqrt {1 - {x^2}} \;
Now, we have all the values of the triangle and can find tan⁡θ\tan \theta .
We know that, tan⁡θ=oppositeadjacent\tan \theta = \dfrac{{opposite}}{{adjacent}}
tan⁡θ=x1−x2\tan \theta = \dfrac{x}{{\sqrt {1 - {x^2}} }}
Putting back the value of θ\theta , we get
tan⁡(sin⁡−1x)=x1−x2\tan \left( {{{\sin }^{ - 1}}x} \right) = \dfrac{x}{{\sqrt {1 - {x^2}} }}
This is the final answer.
So, the correct answer is “ tan⁡(sin⁡−1x)=x1−x2\tan \left( {{{\sin }^{ - 1}}x} \right) = \dfrac{x}{{\sqrt {1 - {x^2}} }} ”.

Note :
sin⁡θ=oppositehypotenuse cos⁡θ=adjacenthypotenuse tan⁡θ=oppositehypotenuse cos⁡ecθ=hypotenuseopposite sec⁡θ=hypotenuseadjacent cot⁡θ=adjacentopposite  \sin \theta = \dfrac{{opposite}}{{hypotenuse}} \\\ \cos \theta = \dfrac{{adjacent}}{{hypotenuse}} \\\ \tan \theta = \dfrac{{opposite}}{{hypotenuse}} \\\ \cos ec\theta = \dfrac{{hypotenuse}}{{opposite}} \\\ \sec \theta = \dfrac{{hypotenuse}}{{adjacent}} \\\ \cot \theta = \dfrac{{adjacent}}{{opposite}} \\\
These are the most basic trigonometric formulas and almost every other formula and relations can be derived from these formulas. So, you must keep these 6 formulas in mind.