Question

How to graph a parabola $y=\left( \dfrac{1}{8} \right){{x}^{2}}$?

Answer 1

First of all convert the given equation of the parabola in the form ${{x}^{2}}=4ay$. Now, to draw the graph of a parabola of the form ${{x}^{2}}=4ay$ first find its vertex by comparing it with the vertex form of the parabola given as ${{\left( x-h \right)}^{2}}=4a\left( y-k \right)$ where (h, k) is the vertex of the parabola. Now, draw an axis of symmetry which will be a vertical line passing through (h, k). In the next step find the concavity of the parabola. If the value of ‘a’ is negative then the parabola is opening downward while for the positive value of ‘a’ the parabola will be opening upwards. Hence, draw the parabola accordingly.

Complete step-by-step answer:
Here we have been provided with the equation of a parabola as $y=\left( \dfrac{1}{8} \right){{x}^{2}}$ and we are asked to draw its graph. Now, to draw the graph of a parabola we need the coordinates of its vertex, axis of symmetry and the nature of concavity of the parabola. Let us find then one by one.
Now, converting the equation of the parabola in the form ${{x}^{2}}=4ay$ we have,
$\begin{aligned} & \Rightarrow {{x}^{2}}=8y \\\ & \Rightarrow {{x}^{2}}=4\times 2\times y \\\ \end{aligned}$
We can write the above equation as: -
$\begin{aligned} & \Rightarrow {{x}^{2}}=8y \\\ & \Rightarrow {{\left( x-0 \right)}^{2}}=4\times 2\times \left( y-0 \right) \\\ \end{aligned}$
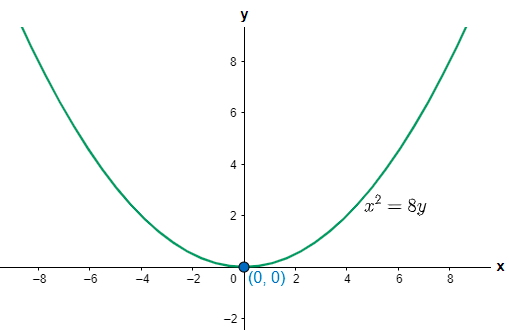
(i) On comparing the above equation with the vertex form of the parabola given as ${{\left( x-h \right)}^{2}}=4a\left( y-k \right)$ where (h, k) is the vertex of the parabola, we get (h, k) = (0, 0). Therefore the vertex of the parabola lies on the origin.
(ii) Now, the axis of symmetry will be the vertical line passing through the point (0, 0), therefore the axis of symmetry is the y axis.
(iii) On comparing the equation${{x}^{2}}=4\times 2\times y$ with ${{x}^{2}}=4ay$ we have a = 2 which is positive, that means the parabola will be opening upwards. So the graph of the given parabola will be shown as below.

Note: Note that we can find the equation of the directrix which is given as y + a = 0 and the length of the latus rectum of the parabola given as $L=4\left| a \right|$. Remember the vertex form of the parabola which is obtained using completing the square method. There is another type of a parabola given by the equation ${{y}^{2}}=4ax$. Here the parabola is opening leftward or rightward and the axis of symmetry is the horizontal line passing through the vertex.