Question

How to graph a parabola $y = \dfrac{1}{2}{(x - 3)^2} + 5$?

Answer 1

In this question, we have an equation and we are supposed to plot a graph after solving it. This can be done when the correct points are found which will be only possible if a table of calculations is made and the values are calculated in order to solve the equation.

Complete step by step answer:
Construct a data table with input $x$ and corresponding values for $y$:
This table will help immensely in understanding the End Behaviour of the given
Function: $y = \dfrac{1}{2}{(x - 3)^2} + 5$

$x$	$y = {x^2}$	$y = {(x - 3)^2}$	$y = \left( {\dfrac{1}{2}} \right){(x - 3)^2}$	$y = (\dfrac{1}{2}){(x - 3)^2} + 5$
Col 1	Col 2	Col 3	Col 4	Col 5
-5	25	64	32.0	37.0
-4	16	49	24.5	29.5
-3	9	36	18.0	23.0
-2	4	25	12.5	17.5
-1	1	16	8.5	13.0
0	0	9	4.5	9.5
1	1	4	2.0	7.0
2	4	1	0.5	5.5
3	9	0	0.0	5.0
4	16	1	0.5	5.5
5	25	4	2.0	7.0

$x: - 5 \leqslant x \leqslant 5$[ Col 1]
Draw graphs for $y = {x^2},y = {(x - 3)^2},y = (\dfrac{1}{2}){(x - 3)^2}$and finally $y = (\dfrac{1}{2}){(x - 3)^2} + 5$
Find Vertices, $x$-intercept and $y$-intercept, if any, for all the graphs.
Step 2
Graph: $y = {x^2}$.....Parent Quadratic Function

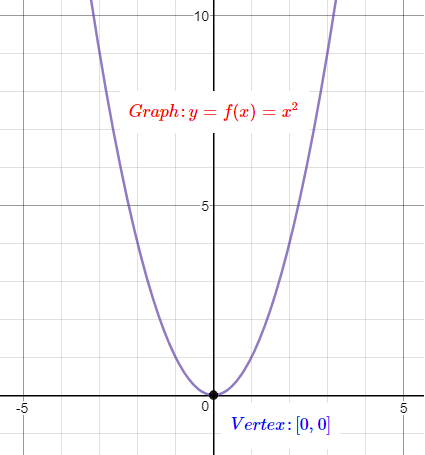
Step 3
Graph: $y = {(x - 3)^2}$

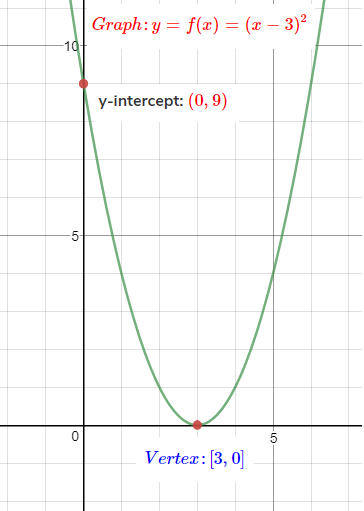
Step 4
Graph: $y = \left( {\dfrac{1}{2}} \right){(x - 3)^2}$

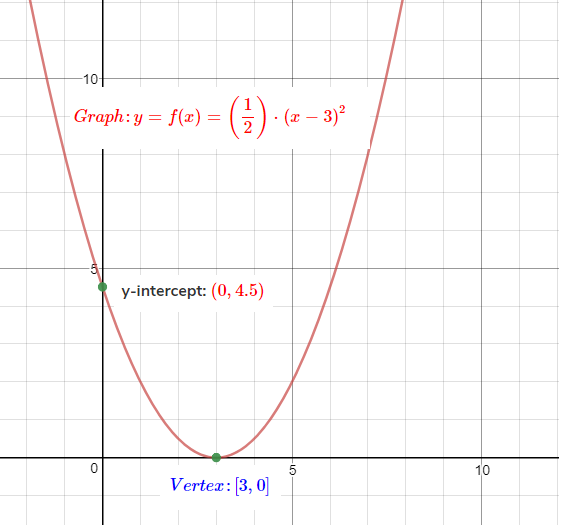
Step 5
Graph: $y = (\dfrac{1}{2}){(x - 3)^2} + 5$

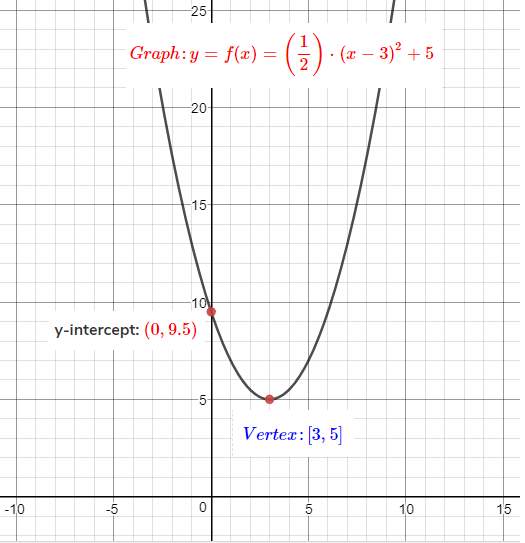
And the last step is to view all the graphs together.
$y = fx = \left( {\dfrac{1}{2}} \right){(x - 3)^2} + 5$

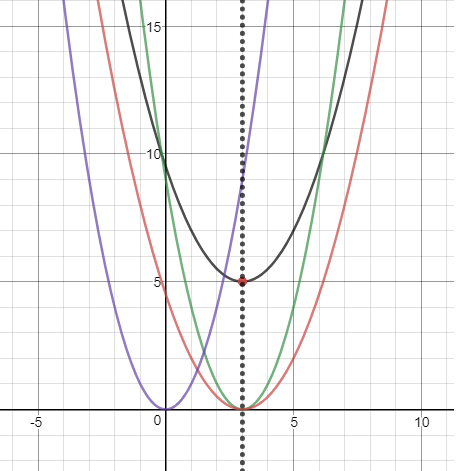
General form: $y = f(x) = a{(x - h)^2} + k,$ Vertex: $(a,h)$
Graph opens up, as the ${x^2}$ term is positive.
Parabolic curve is expanded outward, as $0 < a < 1$
$x = h$ and in our problem $x = 3$ is the Axis of Symmetry
$h = 3$ Indicates the Horizontal Shift
$k = 5$ Indicates the Vertical Shift

Note: The graph of a quadratic function is a U-shaped curve called a parabola. The sign on the coefficient a of the quadratic function affects whether the graph opens up or down. If $a < 0$, the graph makes a frown (opens down) and if $a > 0$then the graph makes a smile (opens up).