Question

How to graph a parabola $y=4{{x}^{2}}$ ?

Answer 1

We have been given the equation of a parabola to be plotted on the cartesian plane. The parent equation of this parabola is ${{x}^{2}}=4y$. We shall first find the vertex of the parabola. Then we shall find multiple points lying on the parabola so that they can be joined together to sketch our final graph.

Complete step by step solution:
Any quadratic equation is of the form $a{{x}^{2}}+bx+c=0$.
However, we are given the equation $y=4{{x}^{2}}$ which represents a parabola.
This equation can also be written as $\left( y-0 \right)=4{{\left( x-0 \right)}^{2}}$. This implies that the coordinates of the vertex of the parabola are $\left( 0,0 \right)$, that is the center of the cartesian plane.
We shall now calculate the points lying on this parabola and tabulate them as follows.

$y=4{{x}^{2}}$	${{x}^{2}}$	$x$
0	$\dfrac{0}{4}$	0
1	$\dfrac{1}{4}$	$\pm \dfrac{1}{2}$
2	$\dfrac{2}{4}$	$\pm \dfrac{1}{\sqrt{2}}$
3	$\dfrac{9}{4}$	$\pm \dfrac{3}{2}$
4	$\dfrac{16}{4}$	$\pm 2$
5	$\dfrac{25}{4}$	$\pm \dfrac{5}{2}$

Dividing 4 from both sides of the equation, $y=4{{x}^{2}}$, we get
${{x}^{2}}=\dfrac{y}{4}$
From this equation, we identify that the given parabola is a vertical parabola.
Thus, plotting the points on the cartesian plane, we get our graph as:

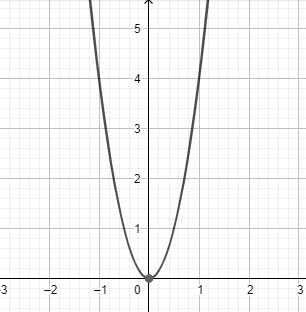
Note:
We know that in order to sketch the graph of a straight-line, we require two points lying on it which can be joined together to draw that straight line. In the case of quadratic equations and curves, only two points cannot suffice and we need more points lying on the curve. Now, since it is mentioned that this curve is that of a parabola, therefore we do not need to find the maxima, minima and points of inflection of the curve.